Чему равно ускорение при вращательном движении

Рассмотрим произвольную точку М твердого тела совершающего вращательное движение, находящуюся на расстоянии R от оси вращения (рис.1.4).

При вращении тела точка М будет описывать окружность радиуса R, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt происходит элементарный поворот тела на угол d 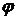, то точка М при этом совершит элементарное перемещение ds=R·d 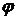. OM=R

v=ds/dt=R·d 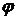/dt или v=ω·R.

Скорость называют линейнойили окружной скоростью точки М.

Направлена скорость по касательной к окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М. При криволинейном движении ее ускорение имеет две составляющих 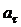и an

; .

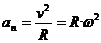Касательная составляющая ускорения направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая всегда направлена по радиусу к оси вращения.

Полное ускорение точки М:

= .

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом μ, который вычисляется по формуле

tg = /an= /ω 2

Задача 1

Угловая скорость тела изменяется по закону 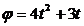. Определить полное ускорение точки тела на расстоянии r=0,25м от оси вращения, в момент времени t=3c.

Так как точка движется по окружности, то ее ускорение можно разложить на составляющие aτ – касательное; an – нормальное.

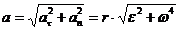
Определим угловую скорость и угловое ускорение точки:

При t1=3c:

Ответ: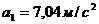

Плоскопараллельное движение твердого тела

Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости П (рис.1.5).

Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси. Прямая плоскости П движется поступательно и для изучения плоского движения достаточно рассмотреть движение плоской фигуры S.

Положение плоской фигуры S в плоскости Оху определяется положением двух произвольных точек А и В этой фигуры (рис.1.6).

Положение отрезка АВ можно определить, зная координаты xA и yA точки А и угол φ, который отрезок АВ образует с осью Oх. Точку A, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.

Для задания плоского движения тела достаточно задать положение полюса А – 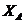, и угла φ

Первые два уравнения определяют поступательное движение вместе с полюсом A. Третье уравнение определяет вращательное движение вокруг оси проходящей через полюс (ось Az).

Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения полюса:

; ; ; ,

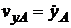а также угловая скорость и угловое ускорение вращательного движения вокруг полюса

; .

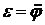Дата добавления: 2018-04-05 ; просмотров: 876 ;

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

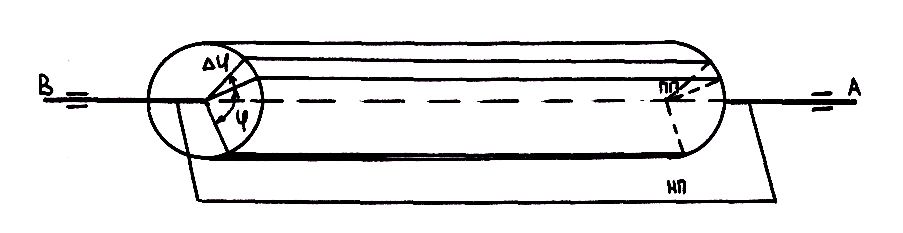
Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

Читайте также:  Совкомбанк череповец личный кабинет

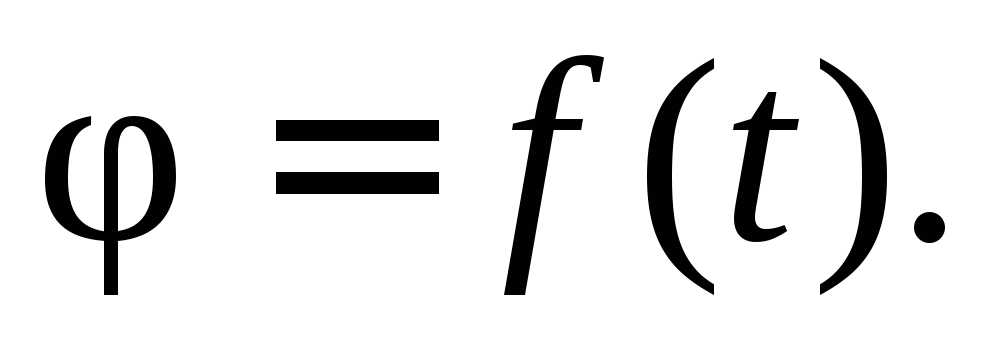
Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина

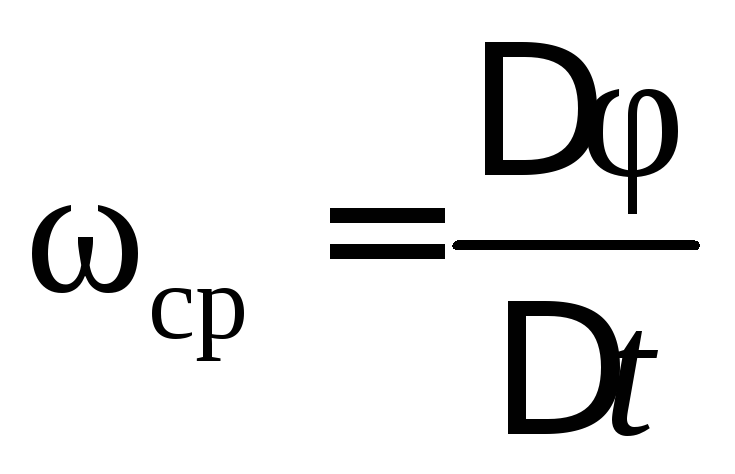
называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;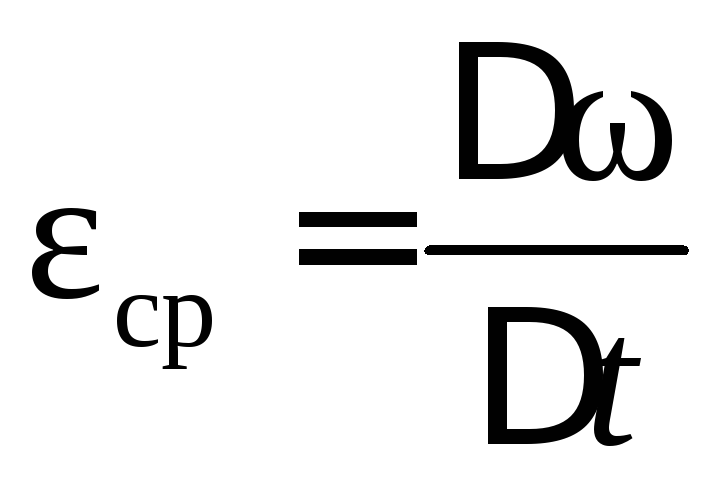

.

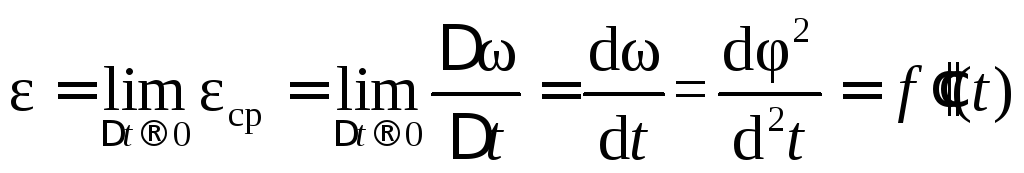Единица углового ускорения 1 рад/с 2 .

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

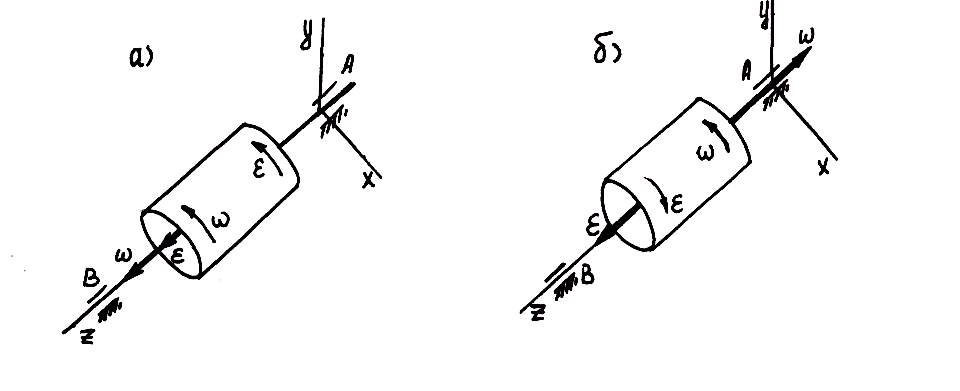
Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение 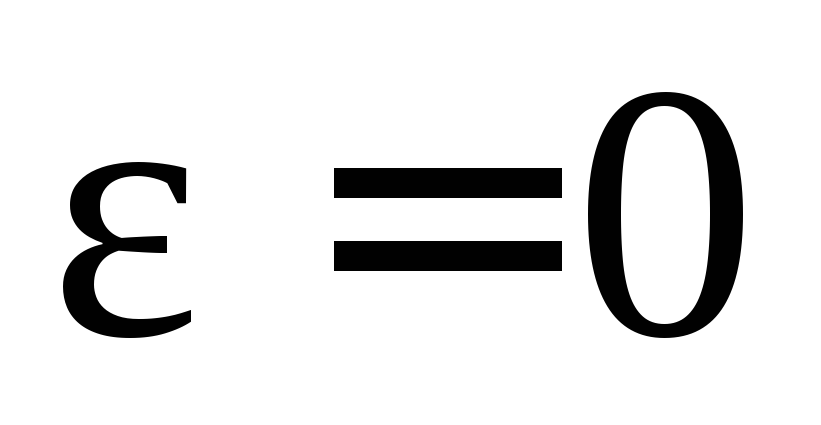и, следовательно, угловая скорость

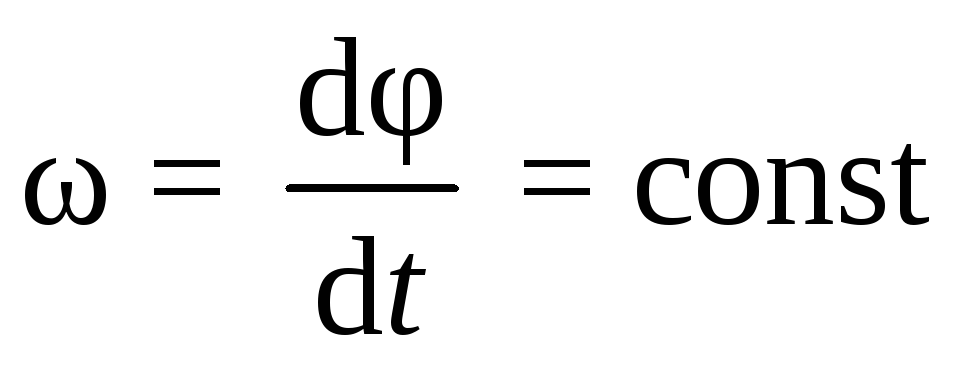, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

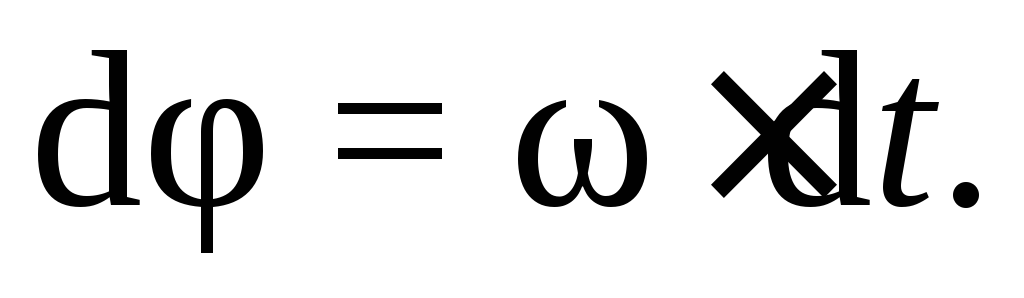
Если при изменении времени от 0 до t угол поворота изменялся от φ (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

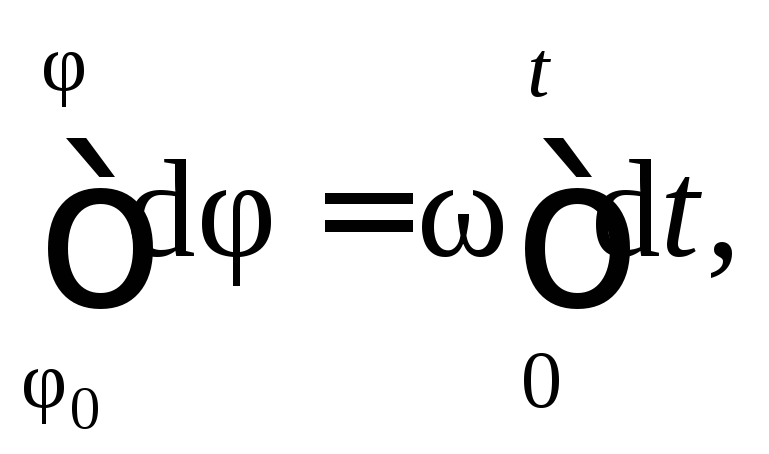
получаем уравнение равномерного вращательного движения

,

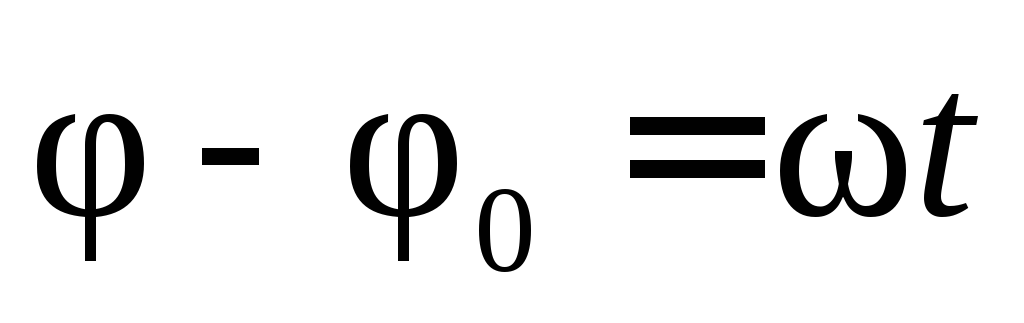которое в окончательном виде записывается так:

.

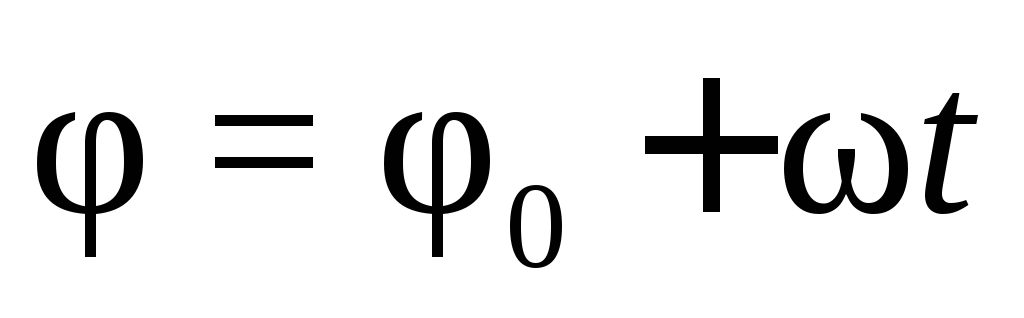Если 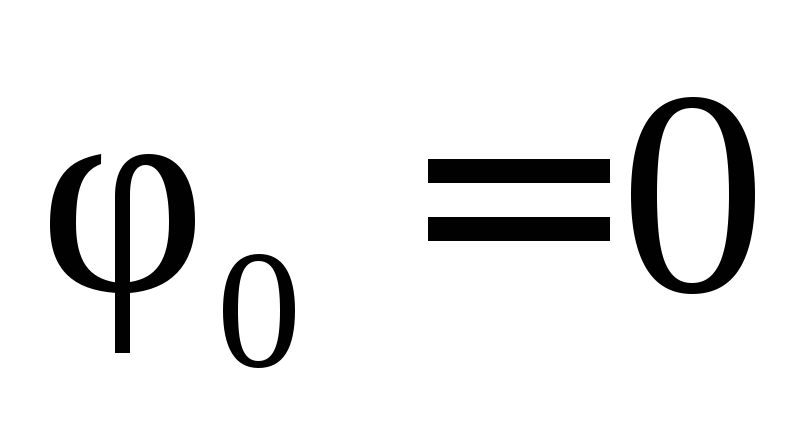, то

.

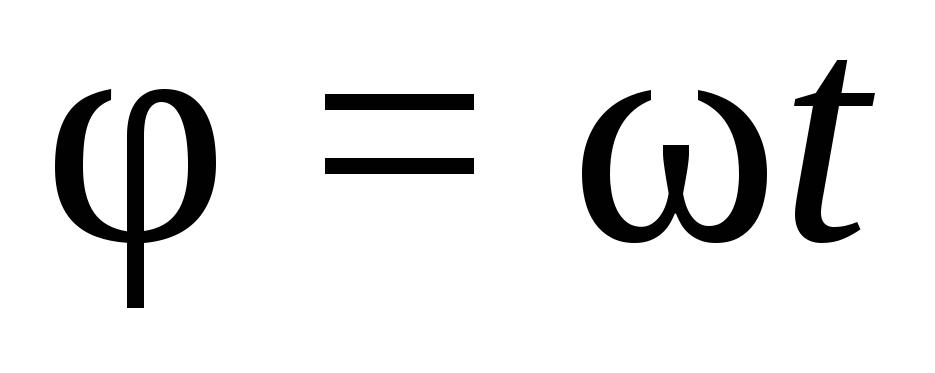Таким образом, при равномерном вращательном движении угловая скорость

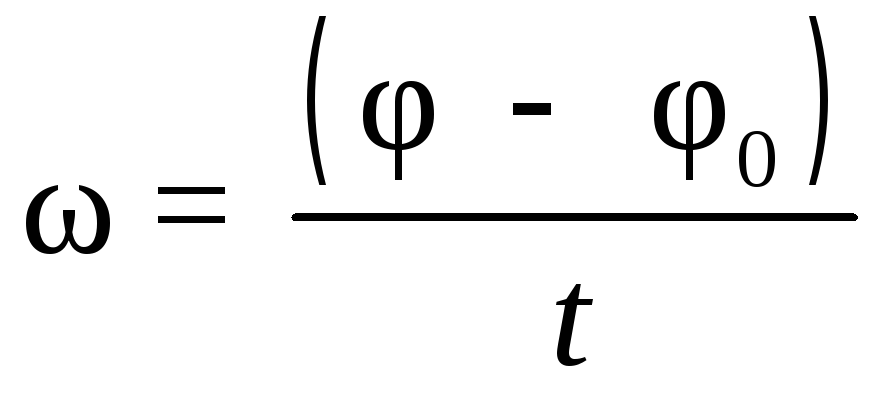или при .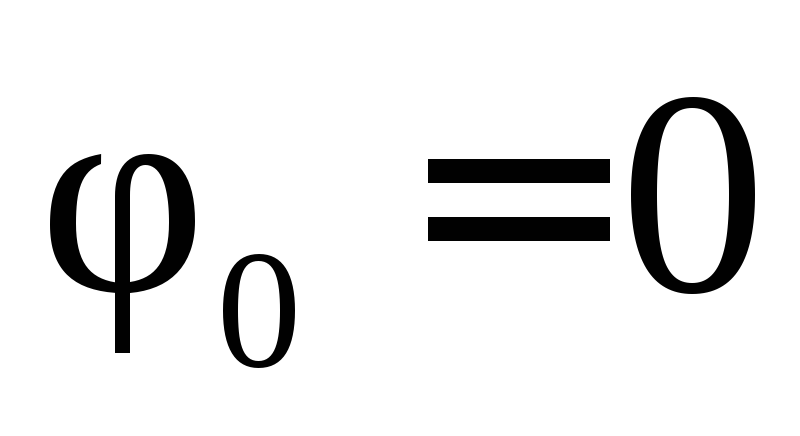

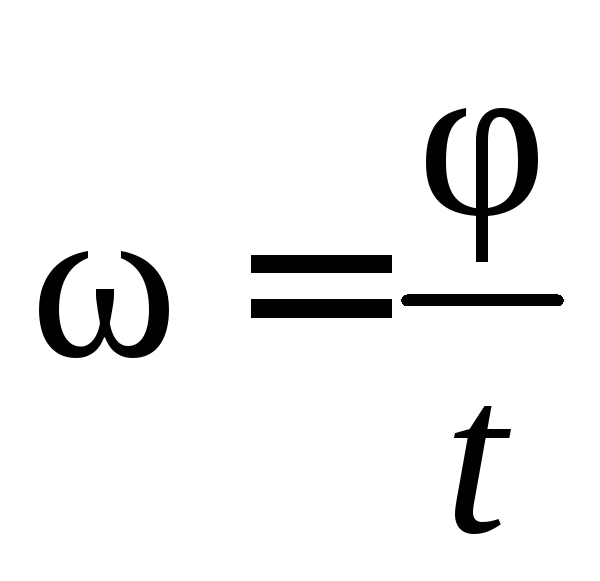2. Равнопеременное вращательное движение. Если угловое ускорение

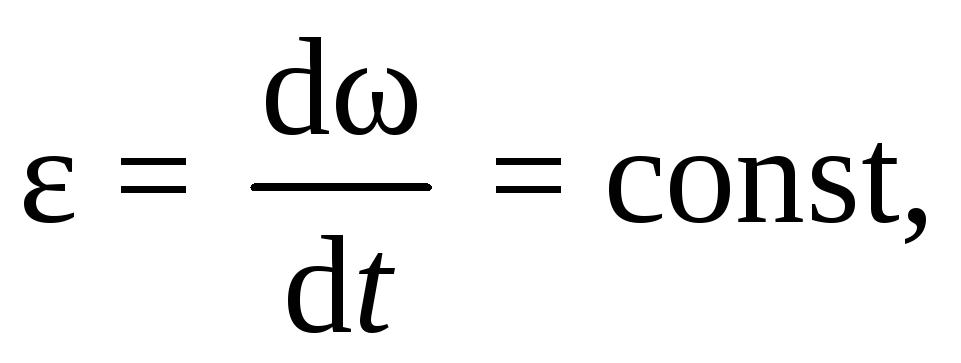(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от 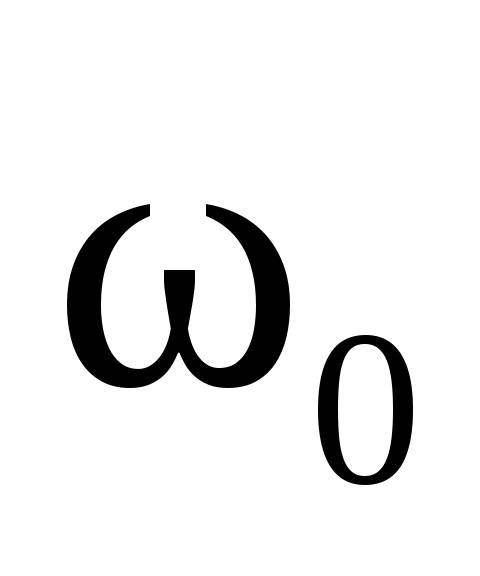(начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

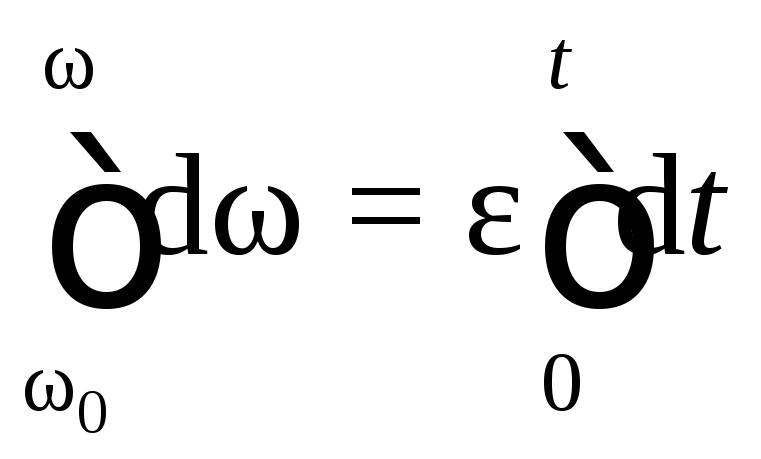или ,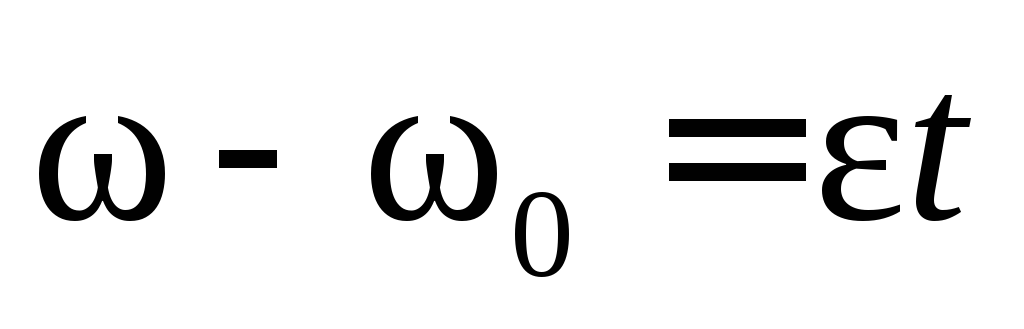

т. е. получим уравнение

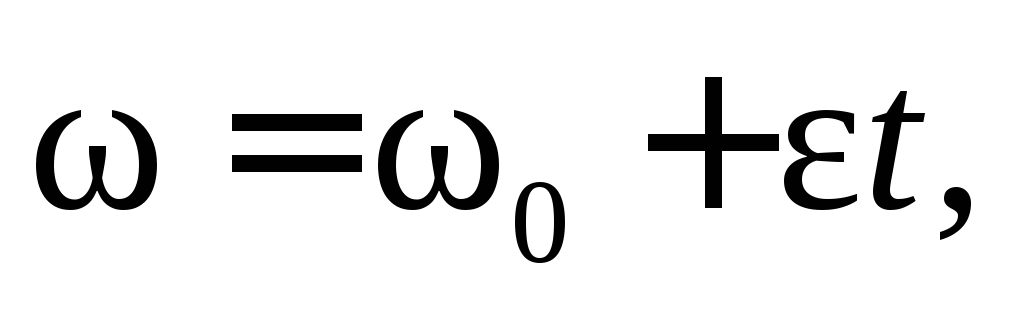(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения 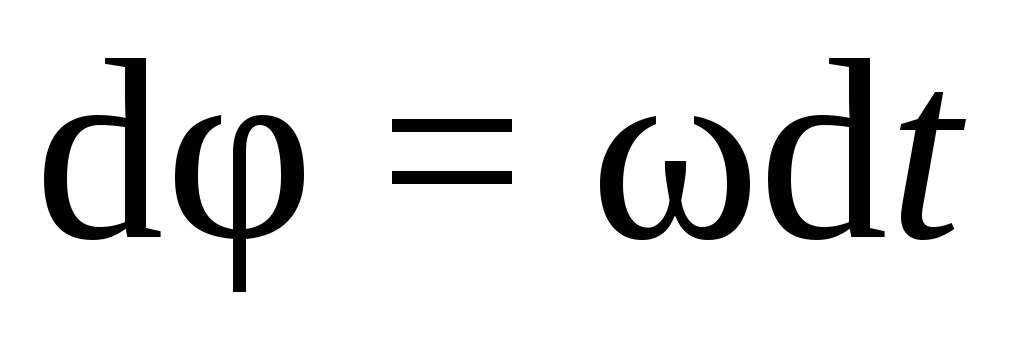или, с учетом уравнения (7.3):

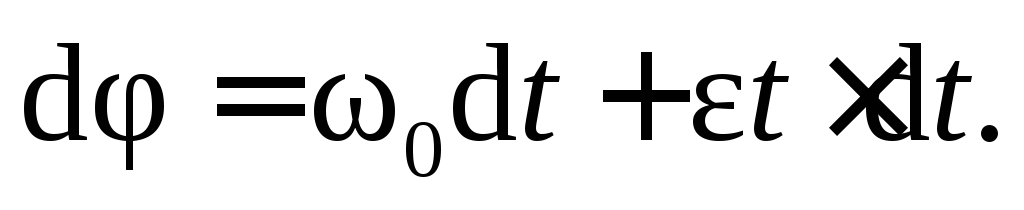
Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

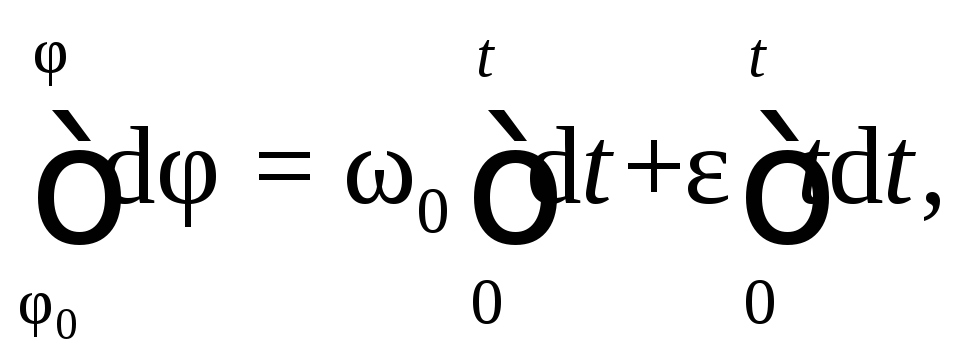или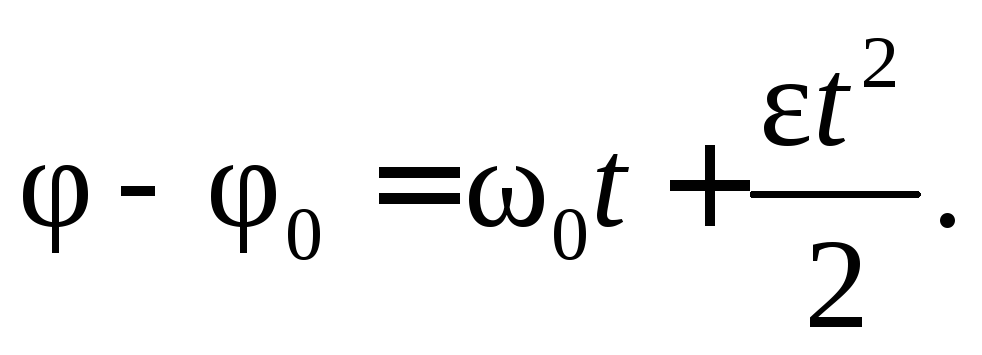

Уравнение равнопеременного вращательного движения в оконча­тельном виде

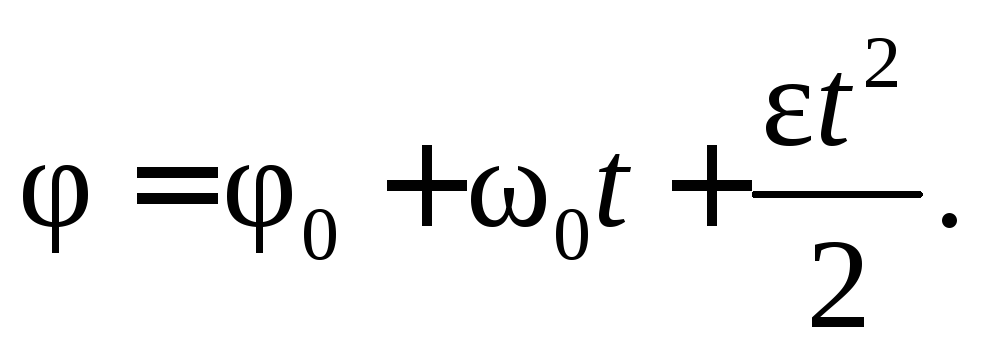(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

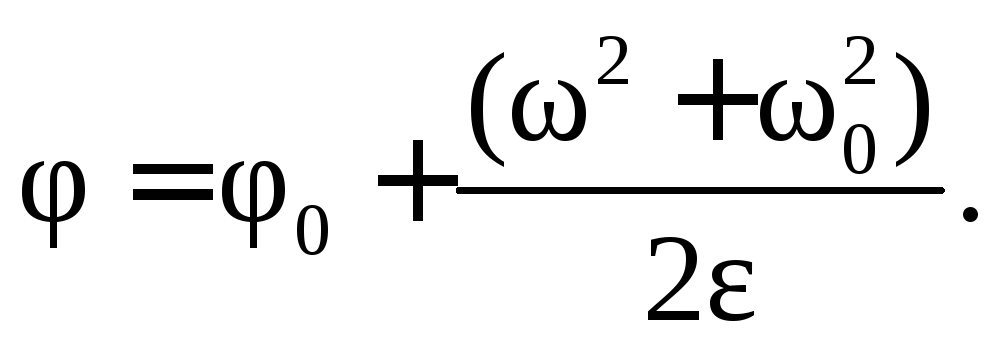(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

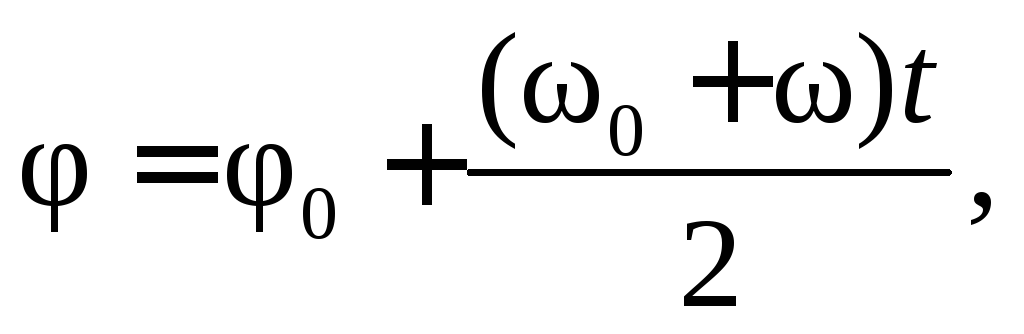(7.6)

где 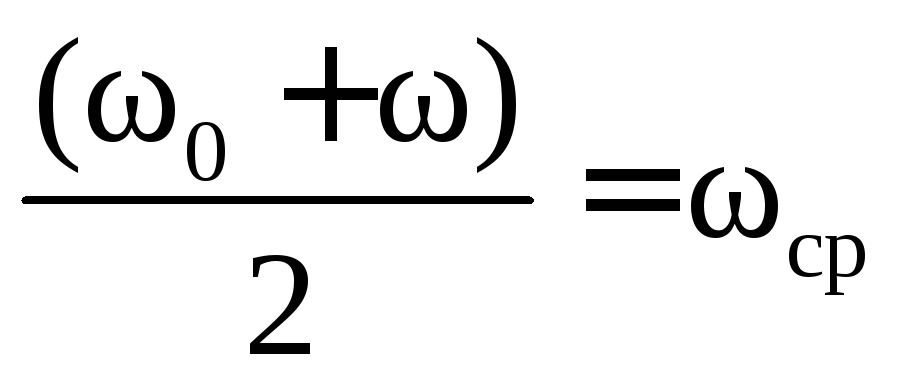– средняя угловая скорость при равнопере­менном вращательном движении.

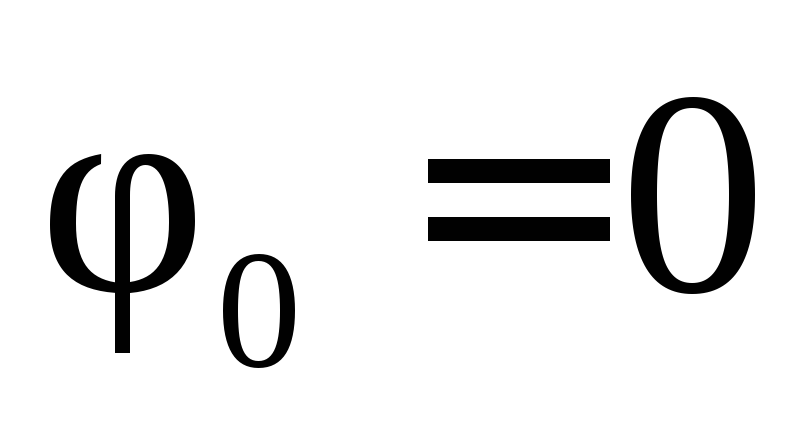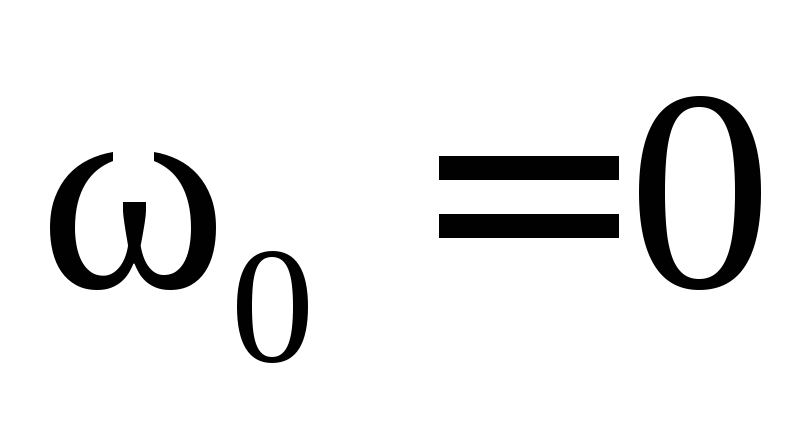Когда и , формулы (7.3)–(7.6) приобретают более простой вид:

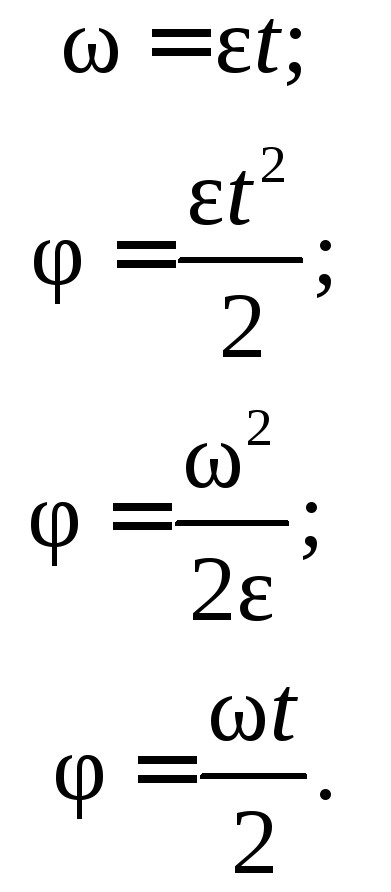
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

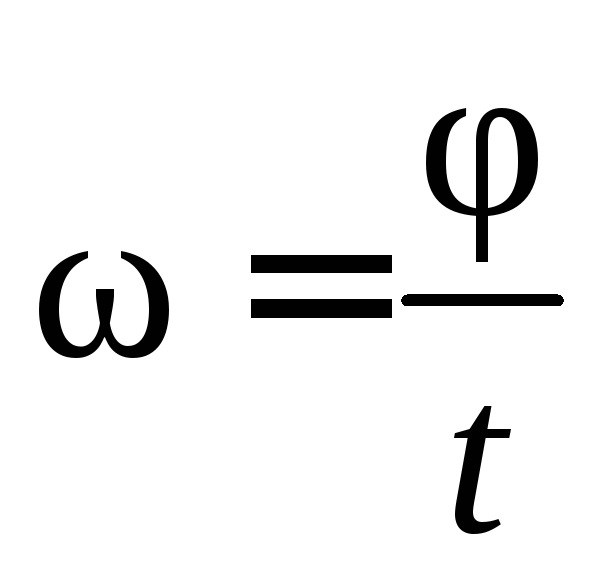Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с –1 ) и n (мин –1 ). Так как , то при n (мин –1 ) за t = 1 мин = 60 с угол поворота 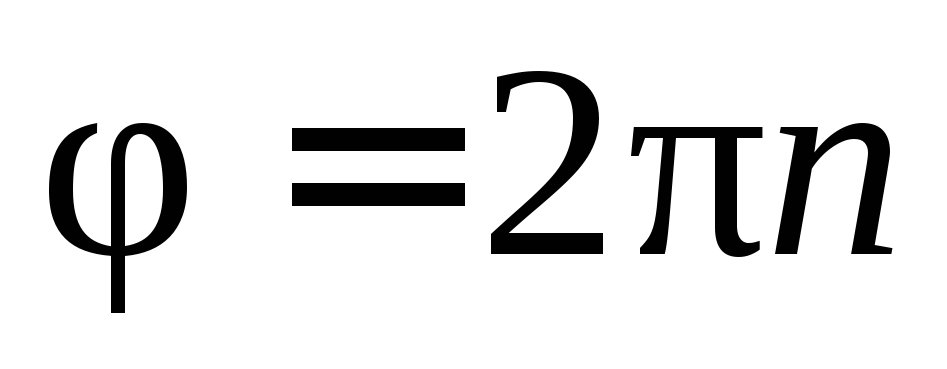. Следовательно:

.

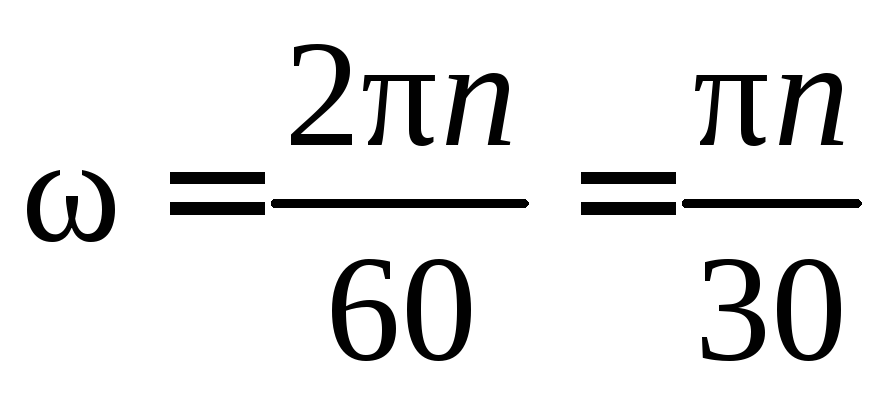При переходе от угловой скорости (с –1 ) к частоте вращения n (мин –1 ) имеем

Читайте также:  Реквизиты виртуальной карты киви

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

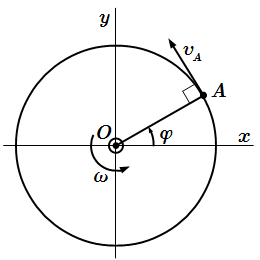
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

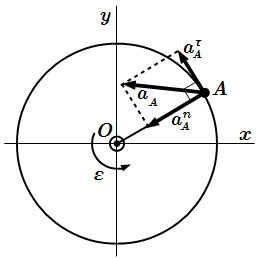
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

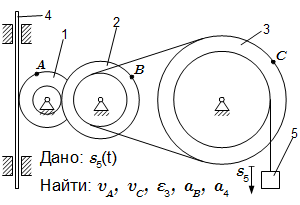
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s5 = t 3 – 6t (см). Положительное направление для s5 – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Читайте также:  Интернет магазин mozilla firefox

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω 1 = 5.3333 с –1 , ω 2 = 1.3333 с –1 , ω 3 = 0.5 с –1 , ε 1 = 10.6667 с –2 , ε 2 = 2.6667 с –2 , ε 3 = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R1 с центром в точке O1, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R3 с центром O3 на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R2 с центром O2, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019