Функция монотонна на неком промежутке, когда она возрастает или убывает на избранном интервале. То есть монотонность функции можно толковать дословно – как ее однообразие.
Функция возрастает на промежутке, когда для всякой пары точек избранного интервала, выраженных соотношением х2 > х1, верно неравенство f (х2) > f (х1). Следовательно, большему значению аргумента соответствует большее значение функции, и её график располагается «снизу вверх».
Урок и презентация по алгебре в 10 классе на тему: «Исследование функции на монотонность. Алгоритм исследования»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Что будем изучать:
1. Убывающие и возрастающие функции.
2. Связь производной и монотонности функции.
3. Две важные теоремы о монотонности.
4. Примеры.
Ребята, ранее мы с вами рассмотрели множество различных функций и строили их графики. Теперь давайте введем новые правила, которое работают для всех функций, которые мы рассматривали и еще будем рассматривать.
Убывающие и возрастающие функции
Функцией называется соответствие y= f(x), в котором каждому значению x ставится в соответствие единственное значение y.
Посмотрим на график некоторой функции:
На нашем графике видно: чем больше x, тем меньше y. Итак, давайте дадим определение убывающей функции. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции.
Если x2 > x1, то f(x2) x1, то f(x2 > f(x1) или: чем больше x, тем больше y.
Если функция возрастает или убывает на некотором промежутке, то говорят, что она монотонна на данном промежутке.
Связь производной и монотонности функции
Если посмотреть на наши касательные или зрительно провести любую другую касательную, то можно заметить, что угол между касательной и положительным направлением оси абсцисс будет острым. Значит, касательная имеет положительный угловой коэффициент. Угловой коэффициент касательной равен значению производной в абсциссе точки касания. Таким образом, значение производной положительно во всех точках нашего графика. Для возрастающей функции выполняет следующее неравенство: f'(x) ≥ 0, для любой точки x.
Читайте также: Выпрямитель с удвоением напряжения расчет
Ребята, теперь давайте посмотрим на график некоторой убывающей функции и построим касательные к графику функции. 
Посмотрим на касательные и зрительно проведем любую другую касательную. Мы заметим, что угол между касательной и положительным направлением оси абсцисс — тупой, а значит касательная имеет отрицательный угловой коэффициент. Таким образом, значение производной отрицательно во всех точках нашего графика. Для убывающей функции выполняет следующее неравенство: f'(x) ≤ 0, для любой точки x.
Итак, монотонность функции зависит от знака производной:
Если функция возрастает на промежутке и имеет производную на этом промежутке, то эта производная будет не отрицательна.
Если функция убывает на промежутке и имеет производную на этом промежутке, то эта производная будет не положительна.
Важно, чтобы промежутки, на которых мы рассматриваем функцию были открытыми!
Две важные теоремы о монотонности
Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f’(x) ≥ 0 (причем равенство производной нулю либо не выполняется, либо выполняется, но лишь в конечном множестве точек), то функция y= f(x) возрастает на промежутке Х.
Теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство f’(x) ≤ 0 (причем равенство производной нулю либо не выполняется, либо выполняется, но лишь в конечном множестве точек), то функция y= f(x) убывает на промежутке Х.
Теорема 3. Если во всех точках открытого промежутка Х выполняется равенство
f’(x)= 0, то функция y= f(x) постоянна на этом промежутке.
Примеры исследования функции на монотонность
1) Доказать, что функция y= x 7 + 3x 5 + 2x — 1 возрастает на всей числовой прямой.
Решение: Найдем производную нашей функции: y’= 7 6 + 15x 4 + 2. Т.к. степень при x четная, то степенная функция принимает только положительные значения. Тогда y’ > 0 для любого x, а значит по теореме 1, наша функция возрастает на всей числовой прямой.
Читайте также: Стиральная машина lg wd 80180s
2) Доказать, что функция убывает: y= sin(2x) — 3x.
Найдем производную нашей функции: y’= 2cos(2x) — 3.
Решим неравенство:
2cos(2x) — 3 ≤ 0,
2cos(2x) ≤ 3,
cos(2x) ≤ 3/2.
Т.к. -1 ≤ cos(x) ≤ 1, значит наше неравенство выполняется для любых x, тогда по теореме 2 функция y= sin(2x) — 3x убывает.
3) Исследовать на монотонность функцию: y= x 2 + 3x — 1.
Решение: Найдем производную нашей функции: y’= 2x + 3.
Решим неравенство:
2x + 3 ≥ 0,
x ≥ -3/2.
Тогда наша функция возрастает при x ≥ -3/2, а убывает при x ≤ -3/2.
Ответ: При x ≥ -3/2 — функция возрастает, при x ≤ -3/2 — функция убывает.
4) Исследовать на монотонность функцию: y= $sqrt<3x — 1>$.
Решение: Найдем производную нашей функции: y’= $frac<3><2sqrt<3x — 1>>$.
Решим неравенство: $frac<3><2sqrt<3x — 1>>$ ≥ 0.
Наше неравенство больше либо равно нуля:
$sqrt<3x — 1>$ ≥ 0,
3x — 1 ≥ 0,
x ≥ 1/3.
Решим неравенство:
$frac<3><2sqrt<3x-1>>$ ≤ 0,
$sqrt<3x-1>$ ≤ 0,
3x — 1 ≤ 0.
Но это невозможно, т.к. квадратный корень определен только для положительных выражений, значит промежутков убывания у нашей функции нет.
Ответ: при x ≥ 1/3 функция возрастает.
Задачи для самостоятельного решения
а) Доказать, что функция y= x 9 + 4x 3 + 1x — 10 возрастает на всей числовой прямой.
б) Доказать, что функция убывает: y= cos(5x) — 7x.
в) Исследовать на монотонность функцию: y= 2x 3 + 3x 2 — x + 5.
г) Исследовать на монотонность функцию: y = $frac<3x-1><3x+1>$.
Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 f (x2).
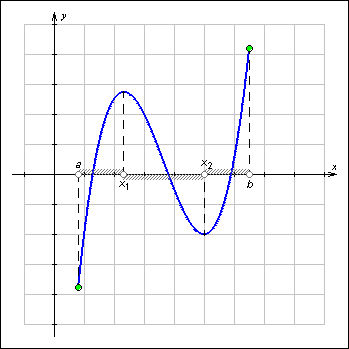Рисунок 1.3.5.1. Промежутки возрастания и убывания функции
На показанном на рисунке графике функция y = f (x),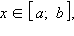 
возрастает на каждом из промежутков [a; x1) и (x2; b] и убывает на промежутке (x1; x2). Обратите внимание, что функция возрастает на каждом из промежутков [a; x1) и (x2; b], но не на объединении промежутков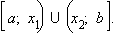 
Читайте также: Кнопка заливки в фотошопе
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.
Действительно, если x1 0) и f + c также возрастают, а функция cf (cn также возрастает.
Аналогичные утверждения можно сформулировать и для убывающей функции.
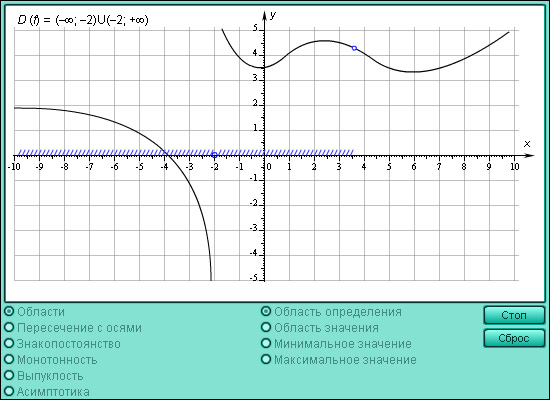Модель 1.9. Свойства функции
Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).
Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).
Точки, в которых достигается максимум или минимум функции, называются точками экстремума.
В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.
Если для любого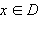 
(x ≠ a) выполняется неравенство f (x) ≤ f (a) 
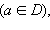то точка a называется точкой наибольшего значения функции на множестве D:
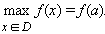
Если для любого 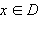(x ≠ b) выполняется неравенство f (x) > f (b) 
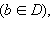то точка b называется точкой наименьшего значения функции на множестве D.
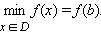
Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.
Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.
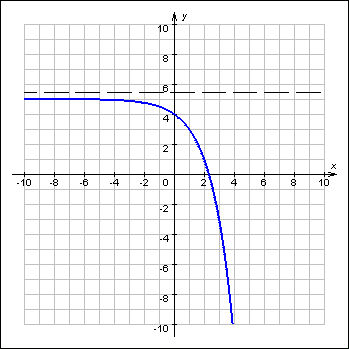График 1.3.5.1. Функция, ограниченная сверху
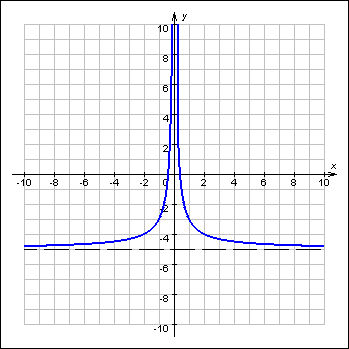График 1.3.5.2. Функция, ограниченная снизу
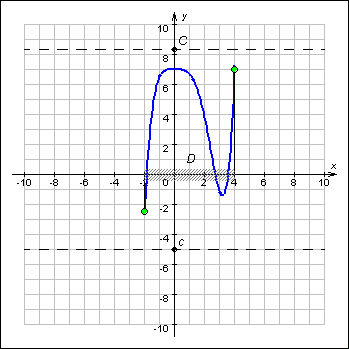График 1.3.5.3. Функция, ограниченная на множестве D.
Наибольшее и наименьшее значения функции y=f(x) на [а,b].
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9966 — 
| 7575 — 
или читать все.
