Система вещественных чисел в математических вычислениях предполагается непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. В следствие этого система вещественных чисел, представимых в машине, является дискретной (прерывной) и конечной.
При написании вещественных чисел в программах вместо привычной запятой принято ставить точку. Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.25 в этой форме можно представить так:
1.25 . 10 0 = 0.125 . 10 1 = 0.0125 . 10 2 = .
12.5 . 10 -1 = 125.0 . 10 -2 = 1250.0 . 10 -3 = . .
Любое число N в системе счисления с основанием q можно записать в виде N = M . q p , где M — множитель, содержащий все цифры числа (мантисса), а p — целое число, называемое порядком. Такой способ записи чисел называется представлением числа с плавающей точкой.
Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:
Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля: 0.12 . 10 3 ;
– 101.01 = – 0.10101 . 2 11 (порядок 112 = 310)– 0.000034 = – 0.34 . 10 -4 ;0.000011 = 0.11 . 2 -100 (порядок —1002 = —410).
Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида:

Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2 k-1 — 1). Например, порядок, принимающий значения в диапазоне от —128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.
Использование смещенной формы позволяет производить операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.
Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.
Стандартные форматы представления вещественных чисел:
1) одинарный – 32-разрядное нормализованное число со знаком, 8-разрядным смещенным порядком и 24-разрядной мантиссой (старший бит мантиссы, всегда равный 1, не хранится в памяти, и размер поля, выделенного для хранения мантиссы, составляет только 23 разряда).
2) двойной – 64-разрядное нормализованное число со знаком, 11-разрядным смещенным порядком и 53-разрядной мантиссой (старший бит мантиссы не хранится, размер поля, выделенного для хранения мантиссы, составляет 52 разряда).
3) расширенный – 80-разрядное число со знаком, 15-разрядным смещенным порядком и 64-разрядной мантиссой. Позволяет хранить ненормализованные числа.
Следует отметить, что вещественный формат с m-разрядной мантиссой позволяет абсолютно точно представлять m-разрядные целые числа, т. е. любое двоичное целое число, содержащее не более m разрядов, может быть без искажений преобразовано в вещественный формат.
Выполнение арифметических действий
над нормализованными числами
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
Сложение и вычитание
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2 -1 и 0.11011 . 2 10 . Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
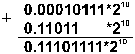
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101 . 2 10 и 0.11101 . 2 1 . Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы:
0.1101 . 2 0 .
Умножение
При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.
Читайте также: Как провести розыгрыш в телеграмме
Пример 3. Выполнить умножение двоичных нормализованных чисел:
(0.11101 . 2 101 ) . (0.1001 . 2 11 ) = (0.11101 . 0.1001) . 2 (101+11) = 0.100000101 . 2 1000 .
Деление
При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.
Пример 4. Выполнить деление двоичных нормализованных чисел:
0.1111 . 2 100 : 0.101 . 2 11 = (0.1111 : 0.101) . 2 (100-11) = 1.1 . 2 1 = 0.11 . 2 10 .
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.


Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Главные правила представления данных в компьютере
Если бы мы могли заглянуть в содержание компьютерной памяти, то увидели бы там примерно то, что условно изображено на рис. 1.5.

Рис. 1.5. Образ компьютерной памяти
Рисунок 1.5 отражает известное вам еще из курса информатики основной школы правило представления данных, которое назовем правилом № 1: данные (и программы) в памяти компьютера хранятся в двоичном виде, т. е. в виде цепочек единиц и нулей.
Современный компьютер может хранить и обрабатывать данные, представляющие информацию четырех видов: числовую, текстовую, графическую, звуковую. Двоичный код, изображенный на рис. 1.5, может относиться к любому виду данных.
Правило № 2: представление данных в компьютере дискретно.
Правило № 3: множество представимых в памяти компьютера величин ограничено и конечно.
Представление чисел
Сначала поясним на образном примере, что такое дискретность.
Дискретное множество состоит из отделенных друг от друга элементов. Например, песок дискретен, поскольку он состоит из отдельных песчинок. А вода или масло непрерывны (в рамках наших ощущений, поскольку отдельные молекулы мы всё равно ощутить не можем). Этот пример нужен нам только для аналогии. Здесь мы не станем углубляться в изучение материального мира, а вернемся к предмету изучения информатики — информации.
Самым традиционным видом данных, с которым работают компьютеры, являются числа. ЭВМ первого поколения умели решать только математические задачи. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными (натуральными) числами: 1, 2, 3, 4, . . Очевидно, что натуральный ряд — это дискретное множество чисел.
В математике ряд натуральных чисел бесконечен и не ограничен. С появлением в математике понятия отрицательного числа (Р. Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел не ограничено как «справа», так и «слева». Покажем это на числовой оси (рис. 1.6), символы оо обозначают бесконечность.

Рис. 1.6. Математическое множество целых чисел на числовой оси
Из сказанного следует вывод: множество целых чисел в математике дискретно и не ограничено. Отметим еще один факт: разность соседних чисел натурального ряда (данного и предыдущего) всегда равна единице. Эту величину назовем шагом числовой последовательности.
Любое вычислительное устройство (компьютер, калькулятор) может работать только с ограниченным множеством целых чисел. Возьмите в руки калькулятор, на индикаторном табло которого помещается 10 знаков. Самое большое положительное число, которое на него поместится:

Самое большое по абсолютной величине (модулю)

Аналогично дело обстоит и в компьютере.
Целые числа в компьютере
Правило № 4: в памяти компьютера числа хранятся в двоичной системе счисления*. С двоичной системой счисления вы знакомы из курса информатики 7-9 классов. Например, если под целое число выделяется ячейка памяти размером в 16 битов, то самое большое целое положительное число будет таким:

В десятичной системе счисления оно равно:
2 15 — 1 = 32 767.
Здесь первый бит играет роль знака числа. Ноль — признак положительного числа. Самое большое по модулю отрицательное число равно -32 768. Напомним (это было в курсе информатики основной школы), как получить его внутреннее представление:
- перевести число 32 768 в двоичную систему счисления; это легко, поскольку 32768 = 2 15 :
1000000000000000;
инвертировать этот двоичный код, т. е. заменить нули на единицы, а единицы — на нули:
0111111111111111;

Единица в первом бите обозначает знак «минус». Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.
Если под целое число в памяти компьютера отводится N битов, то диапазон значений целых чисел:
Читайте также: Найти маршрут на поезде

то есть ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Отсюда же следует и конечность множества целых чисел.
Мы рассмотрели формат представления целых чисел со знаком, т. е. положительных и отрицательных. Бывает, что нужно работать только с положительными целыми числами. В таком случае используется формат представления целых чисел без знака. В этом формате самое маленькое число — ноль (все биты — нули), а самое большое число для 16-разрядной ячейки:

В десятичной системе это 2 16 — 1 = 65 535, примерно в два раза больше по модулю, чем в представлении со знаком.
Из всего сказанного делаем вывод: целые числа в памяти компьютера — это дискретное, ограниченное и конечное множество.
Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака. Шаг в компьютерном представлении последовательности целых чисел, как и в математическом, остается равным единице.
Рисунок 1.7 отражает то обстоятельство, что при переходе от математического представления множества целых чисел к представлению, используемому в информатике (компьютере), происходит переход к ограниченности и конечности.

Рис. 1.7. Представление о множестве целых чисел в математике и в информатике
Вещественные числа в компьютере
Понятие вещественного (действительного) числа в математику ввел Исаак Ньютон в XVIII веке. В математике множество вещественных чисел непрерывно, бесконечно и не ограничено. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел, что и означает непрерывность множества.
Как мы говорили выше, числа в компьютере (в том числе и вещественные) представлены в двоичной системе счисления. Покажем, что множество вещественных чисел в компьютере дискретно, ограничено и конечно. Нетрудно догадаться, что это, так же как и в случае целых чисел, вытекает из ограничения размера ячейки памяти.
Снова для примера возьмем калькулятор с десятиразрядным индикаторным табло. Экспериментально докажем дискретность представления вещественных чисел. Выполним на калькуляторе деление 1 на 3. Из математики вам известно, что 1/3 — это рациональная дробь, представление которой в виде десятичной дроби содержит бесконечное количество цифр: 0,3333333333. (3 в периоде). На табло калькулятора вы увидите:

Первый разряд зарезервирован под знак числа. После запятой сохраняется 8 цифр, а остальные не вмещаются в разрядную сетку (так это обычно называют). Значит, это не точное значение, равное 1/3, а его «урезанное» значение.
Следующее по величине число, которое помещается в разрядную сетку:

Оно больше предыдущего на 0,00000001. Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:

Оно тоже отделено от своего «соседа справа» по числовой оси шагом 0,00000001. Отсюда делаем вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, поскольку числа отделены друг от друга конечными отрезками.
А теперь выясним вот что: будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел)?
Вычислим выражение 100000/3. Получим:

Это число в 100 000 раз больше предыдущего и, очевидно, тоже приближенное. Легко понять, что следующее вещественное число, которое можно получить на табло калькулятора, будет больше данного на 0,0001. Шаг стал гораздо больше.
Отсюда приходим к выводу: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.
Если отметить на числовой оси точные значения вещественных чисел, которые представимы в калькуляторе, то эти точки будут расположены вдоль оси неравномерно. Ближе к нулю — чаще, дальше от нуля — реже (рис. 1.8).

Рис. 1.8. Условное представление взаимного расположения множества вещественных чисел, представимых в компьютере
Все выводы, которые мы делаем на примере калькулятора, полностью переносятся на компьютер с переходом к двоичной системе счисления и с учетом размера ячейки компьютера, отводимой под вещественные числа. Неравномерное расположение вещественных чисел, представимых в компьютере, также имеет место.
Ответим на вопрос: ограничено ли множество вещественных чисел в памяти компьютера? Если продолжать эксперименты с калькулятором, то ответ на этот вопрос будет таким: да, мнолсест-во вещественных чисел в калькуляторе ограничено. Причиной тому служит все та же ограниченность разрядной сетки. Отсюда же следует и конечность множества.
Самое большое число у разных калькуляторов может оказаться разным. У самого простого это будет то же число, что мы получали раньше: 999999999. Если прибавить к нему единицу, то калькулятор выдаст сообщение об ошибке. А на другом, более «умном» и дорогом, калькуляторе прибавление единицы приведет к такому результату:
Читайте также: Телефон отключен подключитесь к itunes как разблокировать

Данную запись на табло надо понимать так: 1 • 10 9 .
Такой формат записи числа называется форматом с плавающей запятой, в отличие от всех предыдущих примеров, где рассматривалось представление чисел в формате с фиксированной запятой.
Число, стоящее перед буквой «е», называется мантиссой, а стоящее после — порядком. «Умный» калькулятор перешел к представлению чисел в формате с плавающей запятой после того, как под формат с фиксированной запятой не стало хватать места на табло.
В компьютере то же самое: числа могут представляться как в формате с фиксированной запятой (обычно это целые числа), так и в формате с плавающей запятой.
Но и для формата с плавающей запятой тоже есть максимальное число. В нашем «подопытном» калькуляторе это число:

То есть 99999 • 10 99 . Самое большое по модулю отрицательное значение -99999 • 10 99 . Данные числа являются целыми, но именно они ограничивают представление любых чисел (целых и вещественных) в калькуляторе.
В компьютере всё организовано аналогично, но предельные значения еще больше. Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.
Рассмотрим пример: пусть под всё число в компьютере выделяется 8 байтов — 64 бита, из них под порядок — 2 байта, под мантиссу — 6 байтов. Тогда диапазон вещественных чисел, в переводе в десятичную систему счисления, оказывается следующим:
±(5 • 10 -324 — 1,7 • 10 308 ).
Завершая тему, посмотрим на рис. 1.9. Смысл, заложенный в нем, такой: непрерывное, бесконечное и не ограниченное множество вещественных чисел, которое рассматривает математика, при его представлении в компьютере обращается в дискретное, конечное и ограниченное множество.

Рис. 1.9. Представление о множестве вещественных чисел в математике и в информатике
Система основных понятий

Вопросы и задания
- Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
- Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.
- Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.
- Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.
- Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
- На какие две части делится число в формате с плавающей запятой?
* Конечно, и «внутри калькулятора» числа представляются в двоичном виде. Однако мы в это вдаваться не будем, рассмотрев лишь внешнее представление. Пример с калькулятором нам нужен был только для иллюстрации проблемы ограниченности.
Большой Энциклопедический словарь . 2000 .
Смотреть что такое «ВЕЩЕСТВЕННОЕ ЧИСЛО» в других словарях:
Вещественное число — в информатике тип данных, содержащий числа, записанные с десятичной точкой и/или с десятичным порядком. См. также: Типы данных Финансовый словарь Финам … Финансовый словарь
вещественное число — действительное число — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы действительное число EN real number … Справочник технического переводчика
Вещественное число — Вещественное, или действительное число [1] математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение… … Википедия
вещественное число — то же, что действительное число. * * * ВЕЩЕСТВЕННОЕ ЧИСЛО ВЕЩЕСТВЕННОЕ ЧИСЛО, то же, что действительное число (см. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО) … Энциклопедический словарь
Вещественное число — то же, что Действительное число … Большая советская энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Математическая энциклопедия
ВЕЩЕСТВЕННОЕ ЧИСЛО — то же, что действительное число … Естествознание. Энциклопедический словарь
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — вещественное число, положительное число, отрицательное число или нуль. Понятие Д. ч. возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики при выражении… … Математическая энциклопедия
Действительное число — вещественное число, любое положительное число, отрицательное число или нуль. Д. ч. разделяются на рациональные и иррациональные. Первые представимы как в виде рациональной дроби, т. е. дроби p/q, где р и q целые, q ≠ 0, так и в виде… … Большая советская энциклопедия
ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО — (вещественное число), любое положит., отрицат. число или нуль. Посредством Д. ч. выражаются результаты измерения всех физ. величин … Естествознание. Энциклопедический словарь
No related posts.








