Пусть дан простой многоугольник (т.е. без самопересечений, но не обязательно выпуклый), заданный координатами своих вершин в порядке обхода по или против часовой стрелки. Требуется найти его площадь.
Способ 1
Это легко сделать, если перебрать все рёбра и сложить площади трапеций, ограниченных каждым ребром. Площадь нужно брать с тем знаком, с каким она получится (именно благодаря знаку вся «лишняя» площадь сократится). Т.е. формула такова:
Способ 2
Можно поступить другим образом. Выберем произвольно точку O, переберём все рёбра, прибавляя к ответу ориентированную площадь треугольника, образованного ребром и точкой O (см. Ориентированная площадь треугольника). Опять же, благодаря знаку, вся лишняя площадь сократится, и останется только ответ.
Этот способ хорош тем, что его проще обобщить на более сложные случаи (например, когда некоторые стороны — не прямые, а дуги окружности).
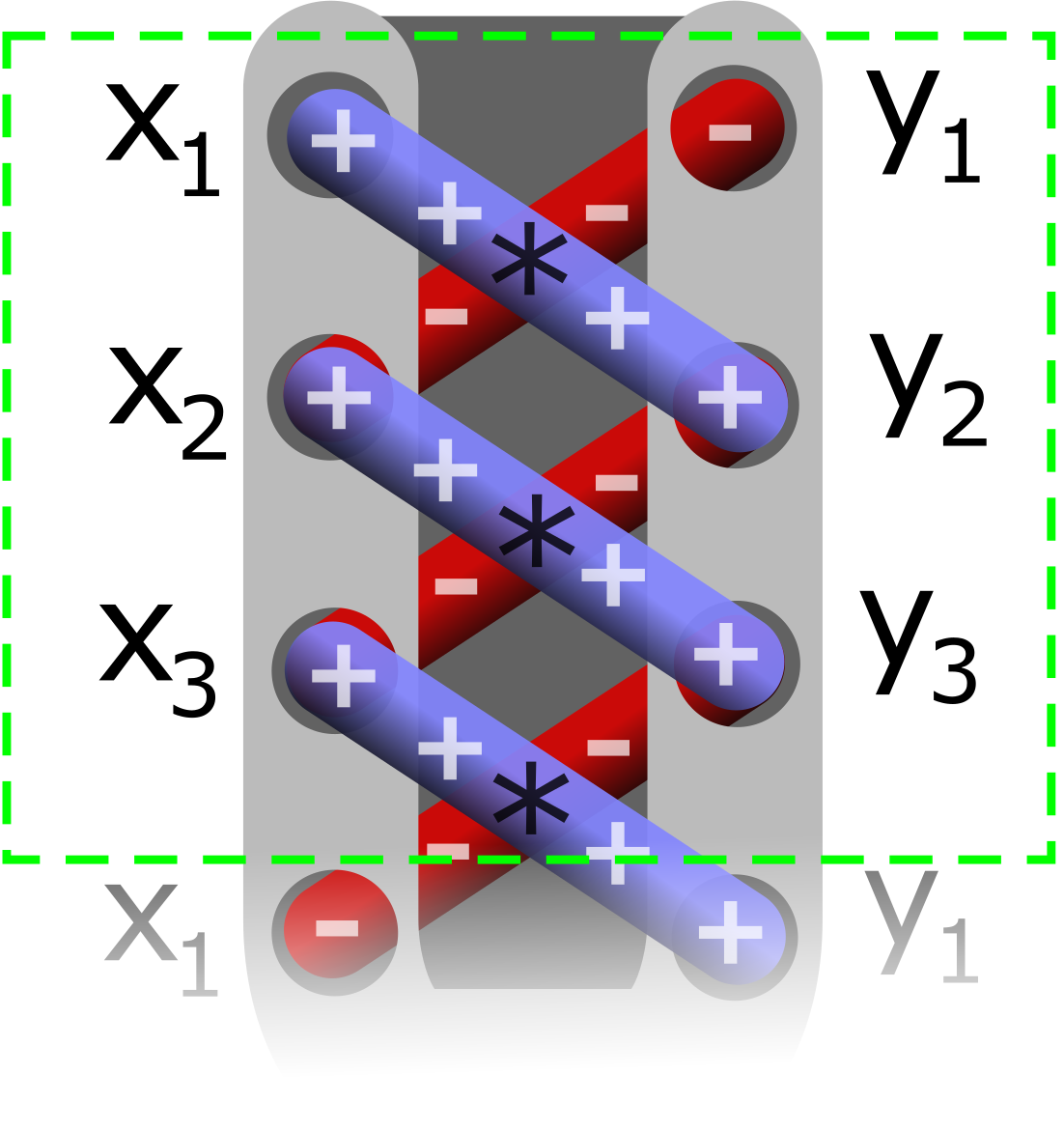
Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. Пользователь перемножает соответствующие координаты и складывает, чтобы найти область, охватывающую многоугольник, и вычитает его из окружающего многоугольника, чтобы найти площадь многоугольника внутри. Это называется формулой шнурков, так как положительные и отрицательные слагаемые из перемножаемых координат располагаются на бумаге крест-накрест, как при завязке шнурков. Она находит применение в геодезии и лесном хозяйстве, среди других областей.
Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.
Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.
Читайте также: Как избавиться от всплывающих окон яндекса
Формула площади верна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым.
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.
где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.
Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5:
Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):
Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:
Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:
и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:
Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».
Материал из Википедии — свободной энциклопедии
Tell your friends about Wikiwand!
Gmail Facebook Twitter Link
Читайте также: Как делают диагностику ноутбука
Suggest as cover photo
Would you like to suggest this photo as the cover photo for this article?
Thank you for helping!
Your input will affect cover photo selection, along with input from other users.








