Определение. Два комплексных числа, имеющие одну и ту же действительную часть и взаимно противоположные коэффициенты мнимых частей, называются взаимно) сопряженными.
Для любого комплексного числа z существует одно и только одно сопряженное с ним комплексное число, которое обозначается . Если , то . Очевидно, тогда и только тогда, когда z — действительное число.
Отметим, что сумма и произведение двух сопряженных комплексных чисел являются действительными числами:
Ранее было выведено правило деления комплексных чисел. Это правило можно проще получить с помощью сопряженных комплексных чисел.
Умножим числитель и знаменатель дроби — на число комплексно сопряженное со знаменателем. Выполнив действия и отделив действительную часть от мнимой, получаем:
Этот результат совпадает с формулой, полученной в п. 6.
Эту формулу можно не запоминать, а только помнить, что при делении надо числитель и знаменатель дроби умножить на число, комплексно сопряженное со знаменателем.
Теорема 1. Число, сопряженное с суммой или произведением комплексных чисел, есть сумма или соответственно произведение чисел, сопряженных данным комплексным числам:
Доказательство. Пусть . Тогда . Имеем:
Эта теорема показывает, что, поставив в соответствие каждому комплексному числу сопряженное с ним число, мы получили взаимно однозначное отображение поля комплексных чисел К на это же поле при котором сохраняются операции сложения и умножения.
Из теоремы 1 непосредственно вытекает следующее
Следствие 1. Число, сопряженное (натуральной) степени комплексного числа, равно той же степени числа, сопряженного данному:
Далее, если нам дан многочлен
коэффициенты которого — комплексные числа, то, заменив каждый коэффициент сопряженным ему комплексным числом мы получим новый многочлен, который обозначим через
Если теперь в полученном многочлене произвольное значение переменной заменить сопряженным ему значением то в силу доказанной выше теоремы и следствия I полученное значение многочлена будет комплексным числом, сопряженным с исходным значением многочлена
Если, в частности, все коэффициенты многочлена действительные числа, то один и тот же многочлен, и формула (3) дает:
Таким образом, мы получили
Следствие 2. При замене в многочлене с действительными коэффициентами произвольного значения аргумента сопряженным ему числом значение многочлена также заменяется сопряженным ему числом.
Читайте также: Vkfeed как включить невидимку
Определение. Комплексным числом z называется выражение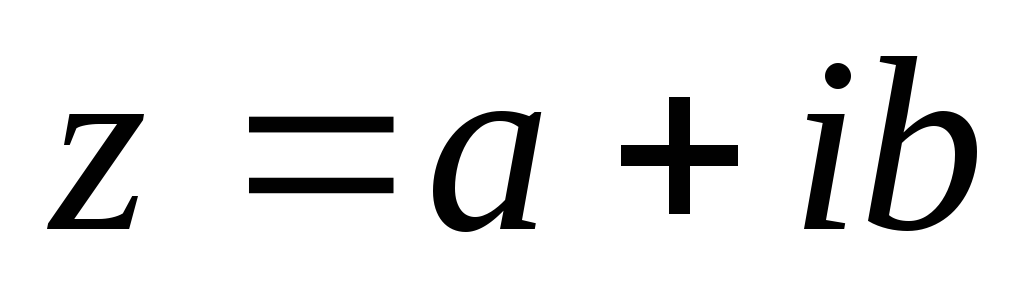 
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
При этом число a называется действительной частью числа z (a = Re z), а b— мнимой частью (b = Im z).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа 
и 
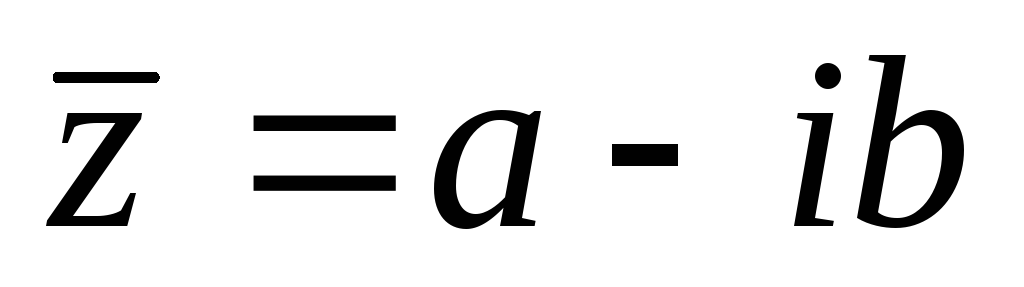называются комплексно – сопряженными.
Определение. Два комплексных числа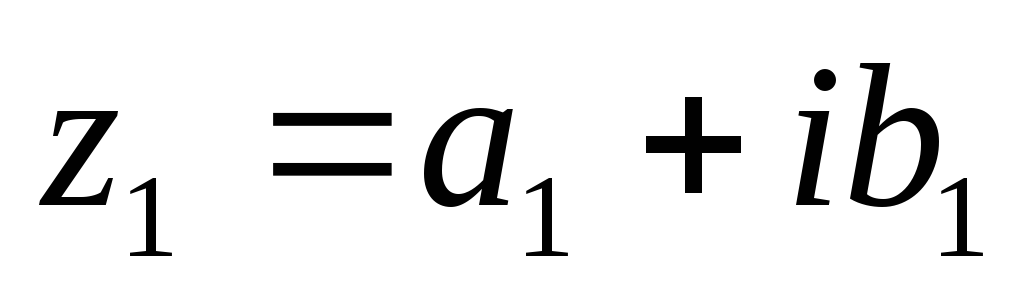 
и 
называются равными, если соответственно равны их действительные и мнимые части:
Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
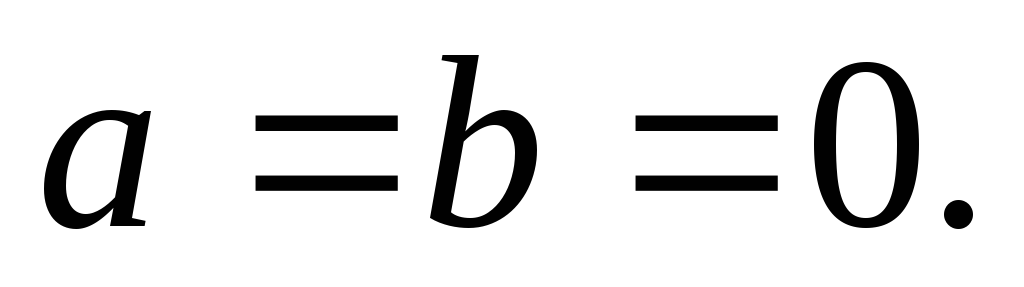
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная — мнимой осью.
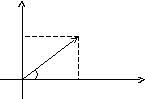
Таким образом, на оси Оx располагаются действительные числа, а на оси Оy – чисто мнимые.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма комплексного числа.
Из геометрических соображений видно, что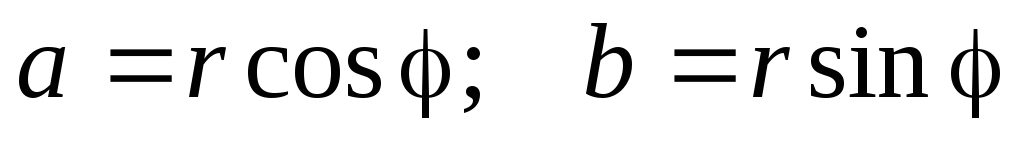 
. Тогда комплексное число можно представить в виде:
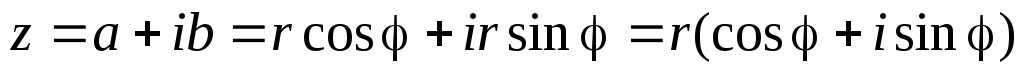
Такая форма записи называется тригонометрической формой записи комплексного числа.
При этом величина r называется модулем комплексного числа, а угол — аргументом комплексного числа.
.
Из геометрических соображений видно:
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.
Действия с комплексными числами.
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание.
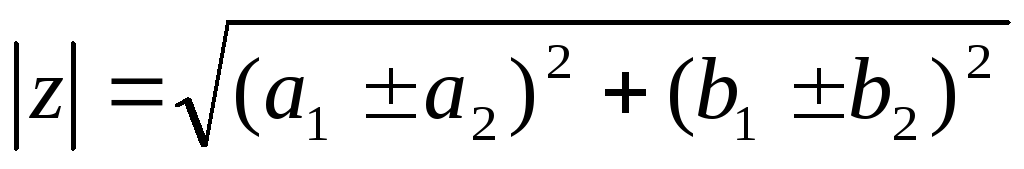
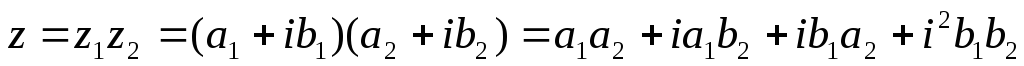
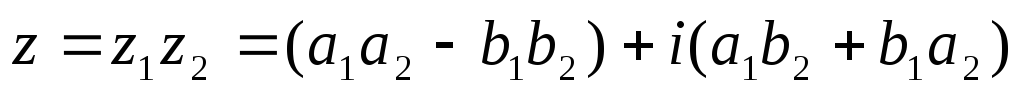
В тригонометрической форме:
, 
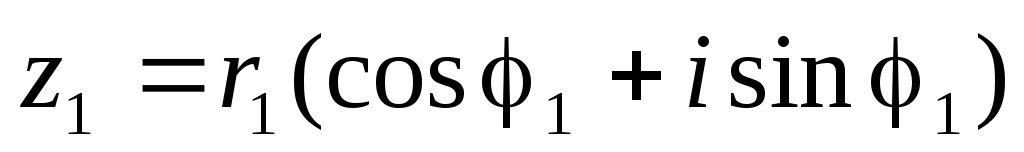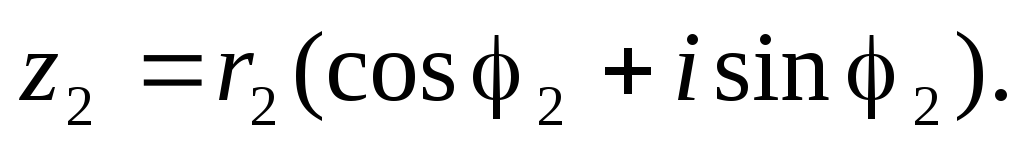
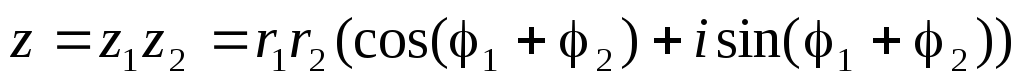
С случае комплексно – сопряженных чисел:
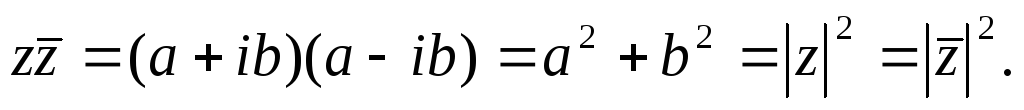
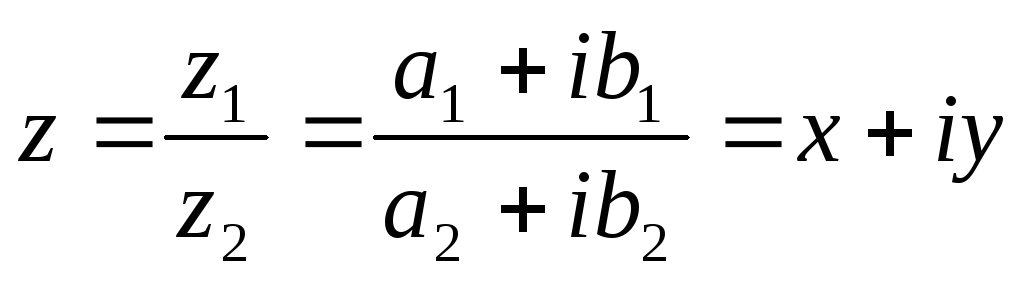
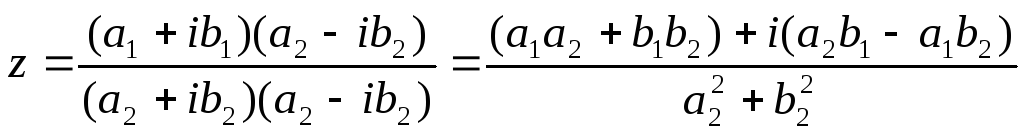
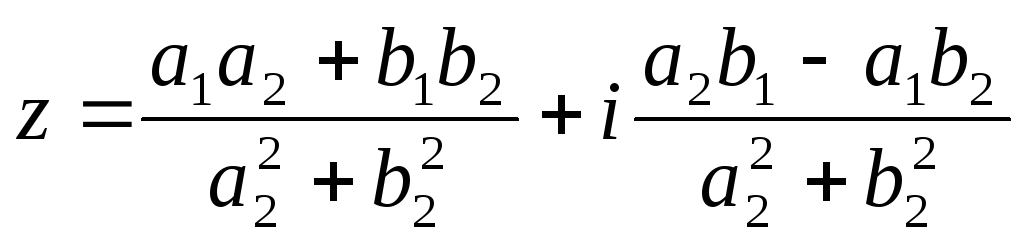
В тригонометрической форме:
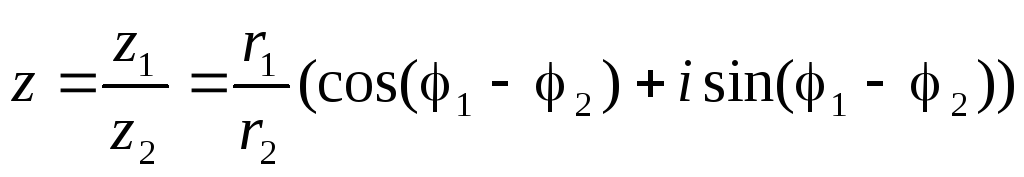
4) Возведение в степень.
Из операции умножения комплексных чисел следует, что
Читайте также: Как установить lmod на samsung
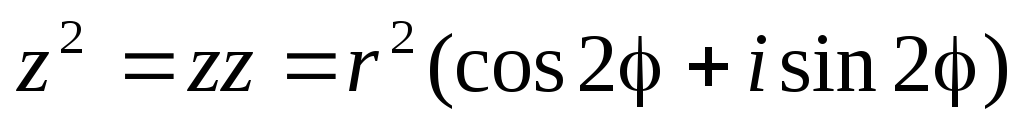
В общем случае получим:
,
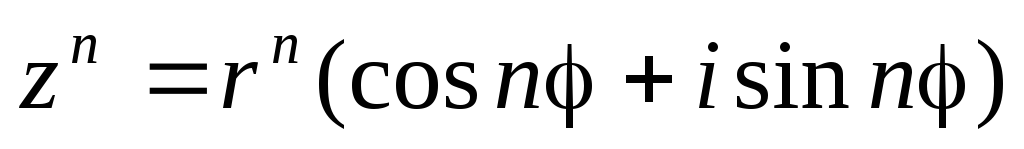где n – целое положительное число.
Это выражение называется формулой Муавра. (Абрахам де Муавр (1667 – 1754) – английский математик)
Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.
Пример. Найти формулы sin2 и cos2.
Рассмотрим некоторое комплексное число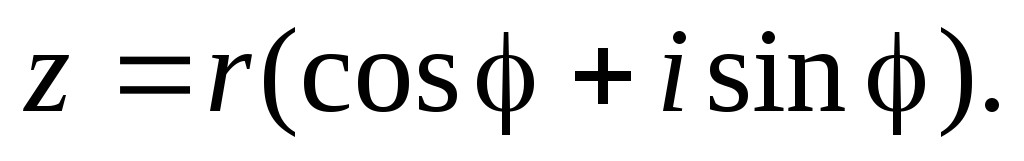 
Тогда с одной стороны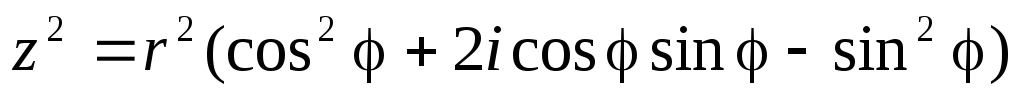 
.
По формуле Муавра: 
Приравнивая, получим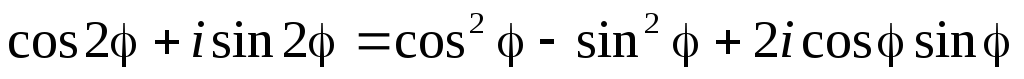 
Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то
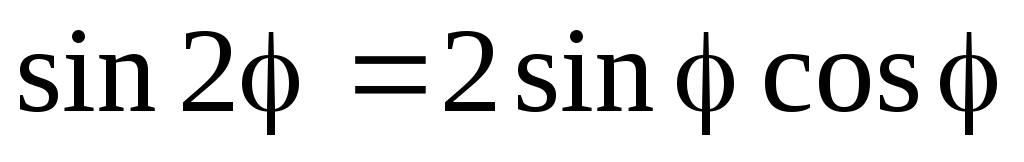
Получили известные формулы двойного угла.
5) Извлечение корня из комплексного числа.
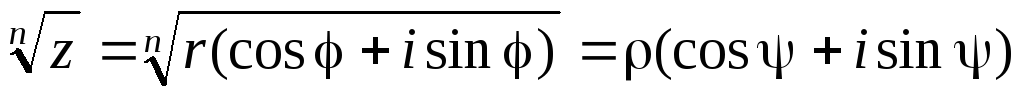
Возводя в степень, получим:
Отсюда: 
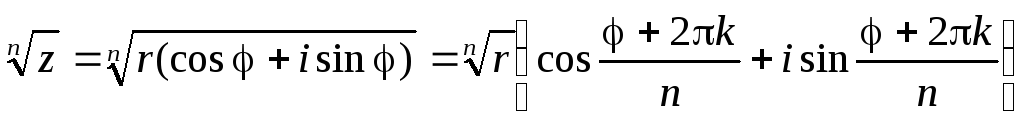
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений для k=0,1. n-1.
Показательная форма комплексного числа.
Рассмотрим показательную функцию 
Можно показать, что функция w может быть записана в виде:
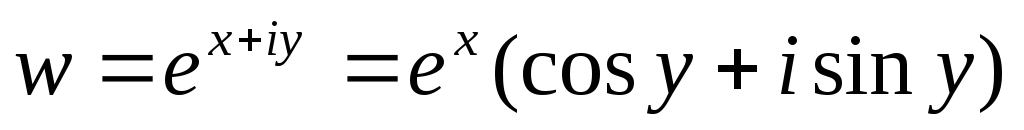
Данное равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен позднее.
Для комплексных чисел будут справедливы следующие свойства:
1) 
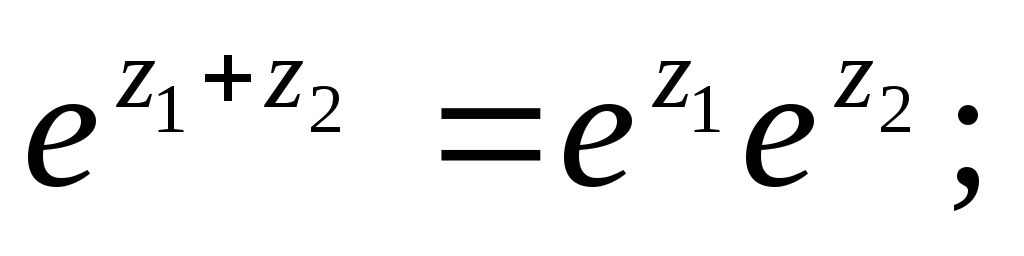
2) 
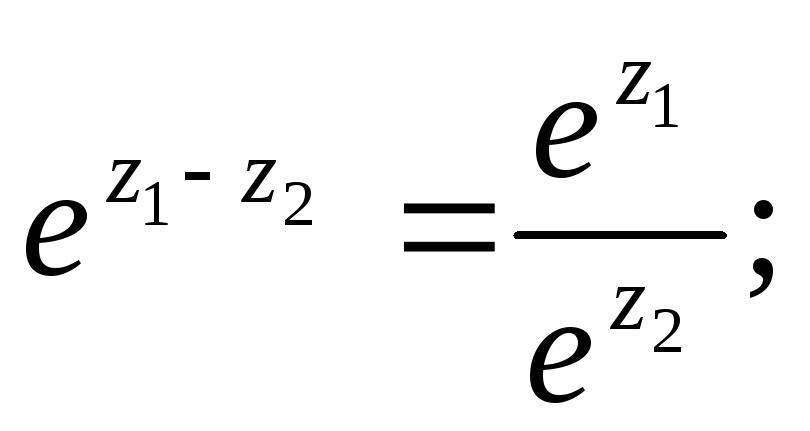
3) 
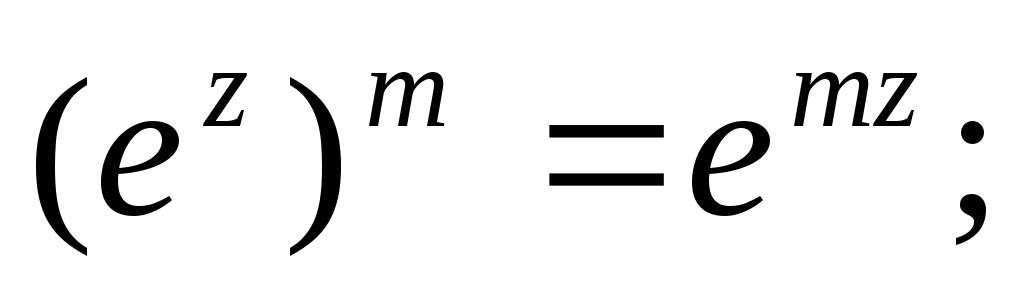где m – целое число.
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:
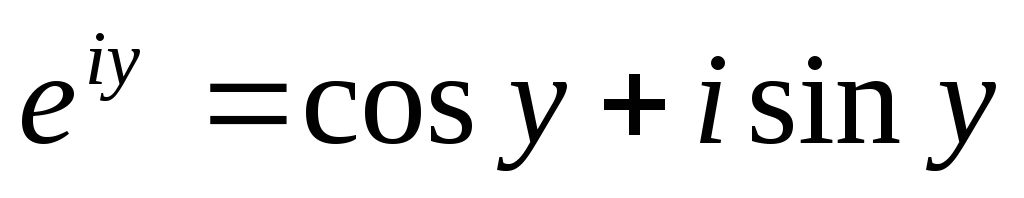
Для комплексно – сопряженного числа получаем:
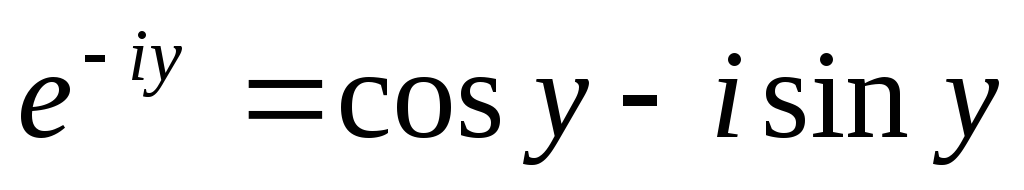
Из этих двух уравнений получаем:
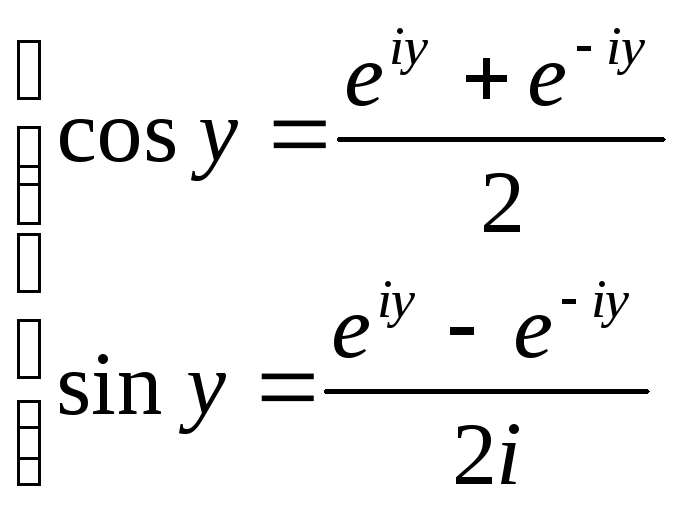
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.
Если представить комплексное число в тригонометрической форме:
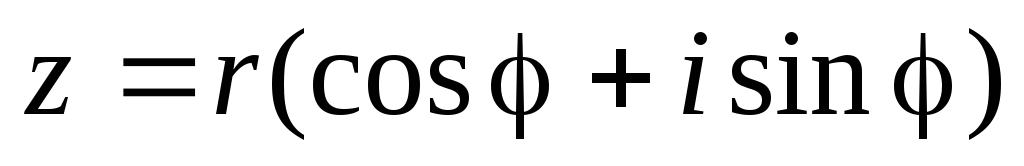
и воспользуемся формулой Эйлера: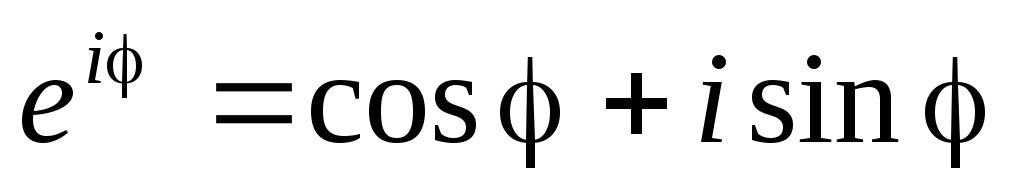 
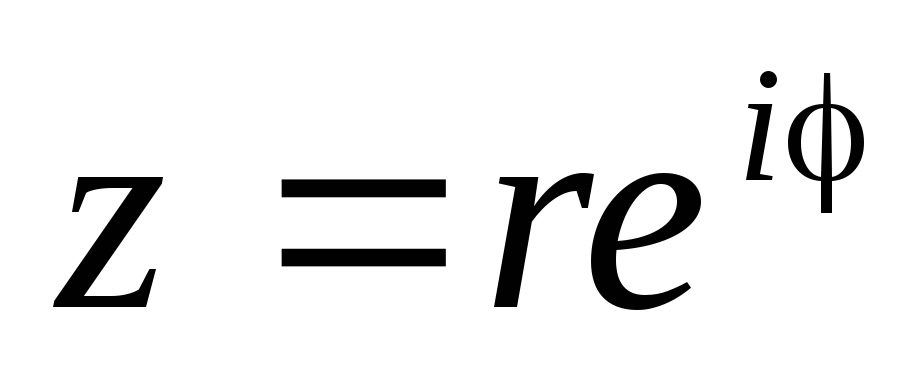
Полученное равенство и есть показательная форма комплексного числа.
Разложение многочлена на множители.
Определение. Функция вида f(x)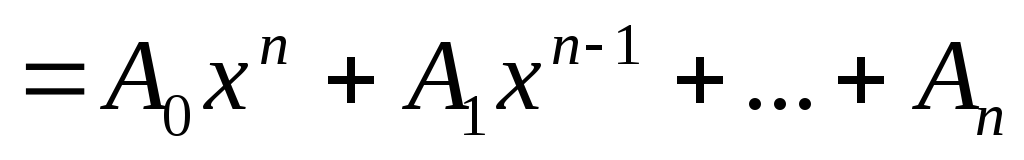 
называется целой рациональной функцией от х.
Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)
При делении многочлена f(x) на разность x – a получается остаток, равный f(a).
Доказательство. При делении многочлена f(x) на разность x – a частным будет многочлен f1(x) степени на единицу меньшей, чем f(x), а остатком – постоянное число R.
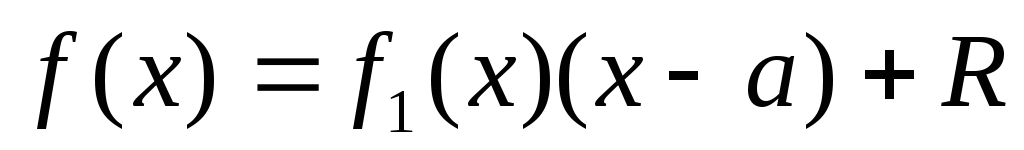
Следствие. Если, а – корень многочлена, т.е. f(a) = 0, то многочлен f(x) делится на (х – а) без остатка.
Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f(x) имеет, по крайней мере, один корень, действительный или комплексный.
Читайте также: Dexp софт для мышки
Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида (x – a) и множитель, равный коэффициенту при x n .
Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:
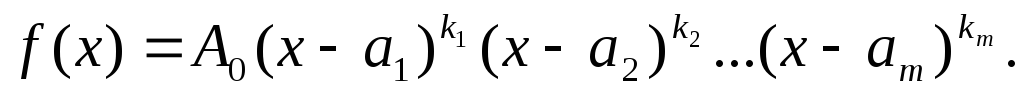
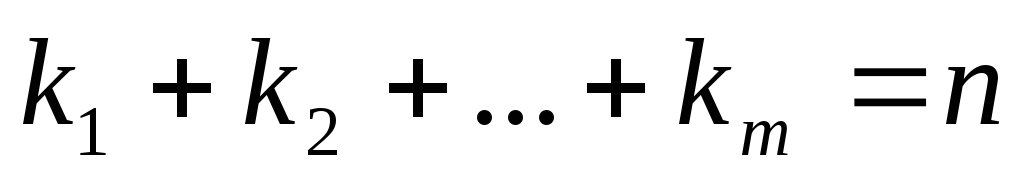
ki — кратность соответствующего корня.
Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).
Это свойство имеет большое значение для решения алгебраических уравнений, дифференциальных уравнений и играет важную роль в анализе функций.
Рассмотрим несколько примеров действий с комплексными числами.
Пример. Даны два комплексных числа 
. Требуется а) найти значение выражения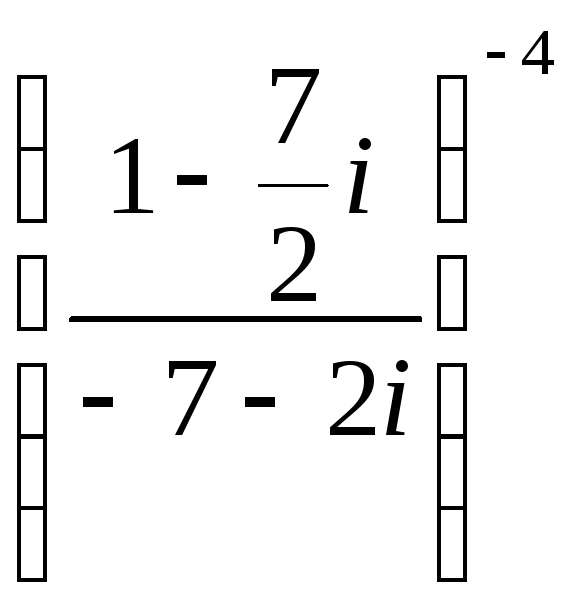 
в алгебраической форме, б) для числа 
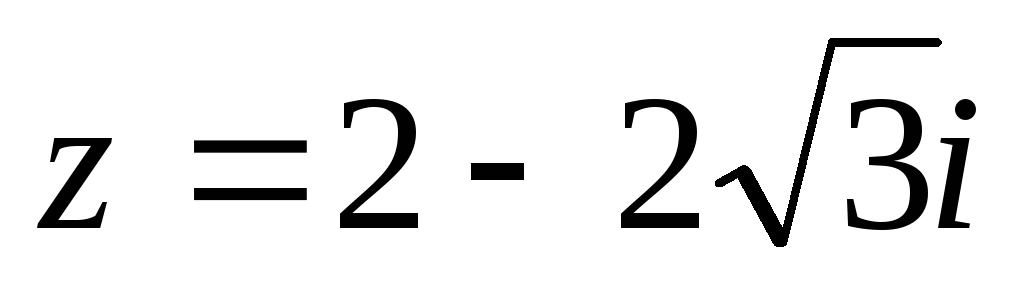найти тригонометрическую форму, найти z 20 , найти корни уравнения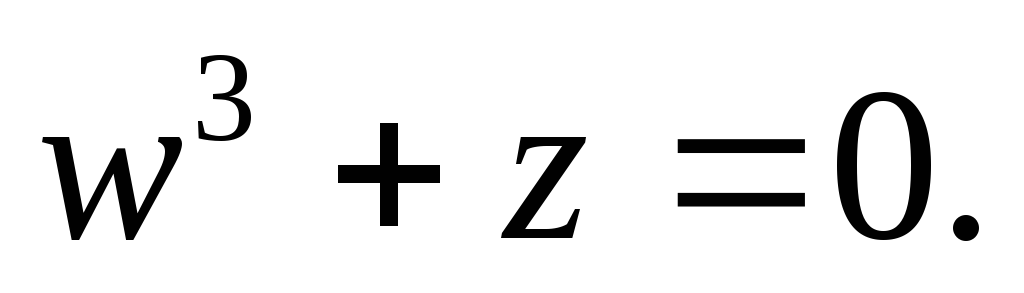 
Очевидно, справедливо следующее преобразование:
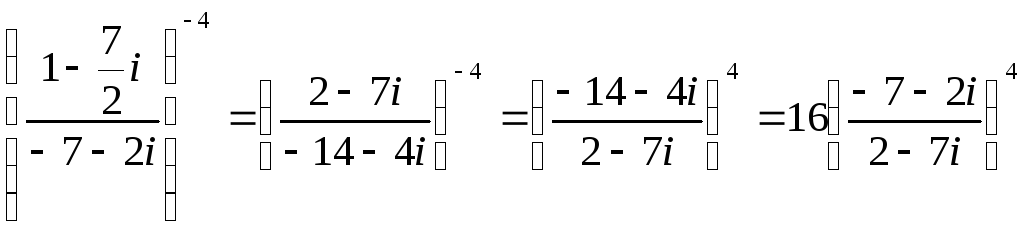
Далее производим деление двух комплексных чисел:
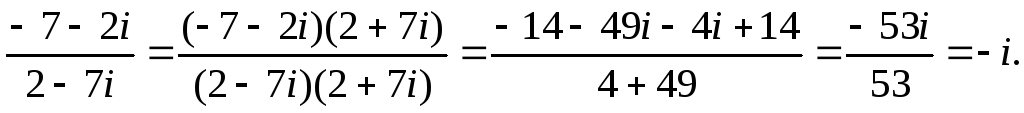
Получаем значение заданного выражения: 16(-i) 4 = 16i 4 =16.
б) Число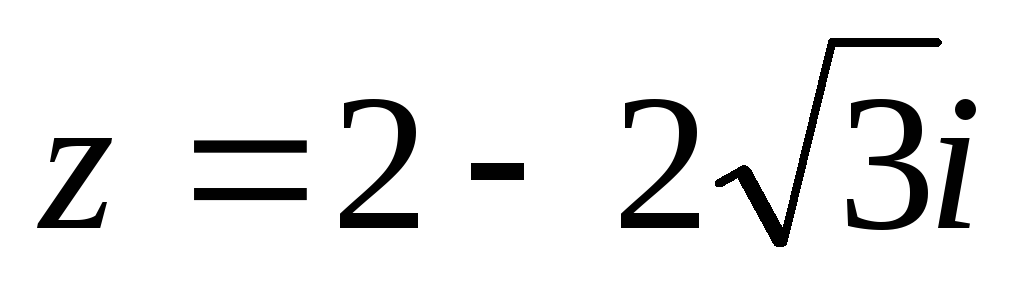 
представим в виде 
, где
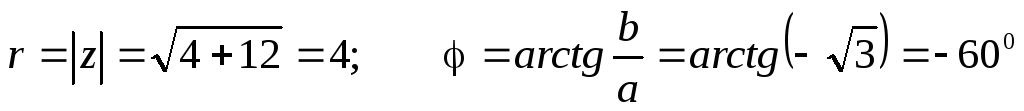
Тогда 
.
Для нахождения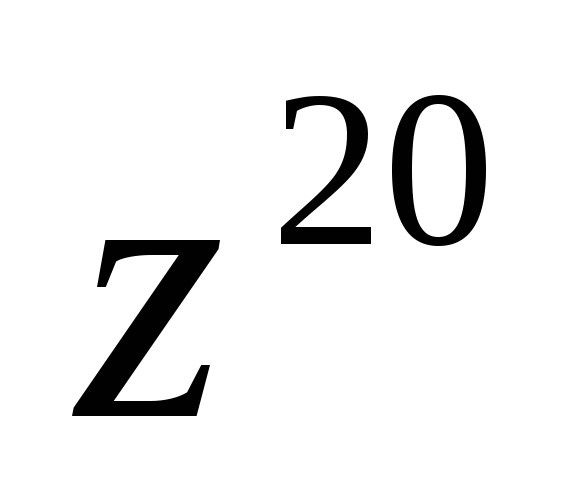 
воспльзуемся формулой Муавра.
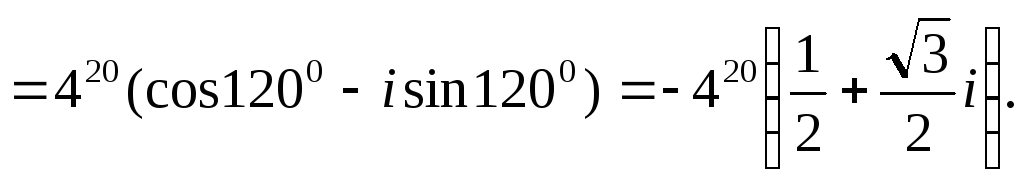
Если 
, то 
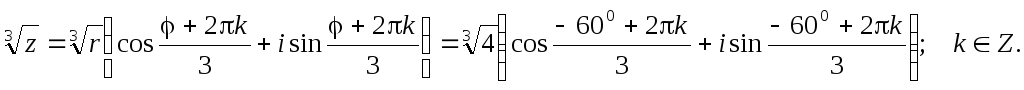
Подставляя последовательно k=0, k=1 и k=2 и производя вычисления получим 3 значения корня кубического.
Единственность алгебраической формы.
Об отношении линейного порядка на множестве комплексных чисел
Свойства комплексных чисел рассматриваются в курсе алгебры и теории чисел (см., например, [5]), поэтому здесь мы рассмотрим лишь два принципиально важных свойства.
6.2.1. Теорема. Алгебраическая форма комплексного числа единственна.
Доказательство. Пусть a+bi=c+di, я,6,с,с/ е R, докажем, что а = с, b = d. Имеем: a-c = (d-b)i. Если предположить, что b*d,
то / =-— е R, что невозможно, гак как квадрат любого
действительного числа неотрицателен. Следовательно, b = d, откуда а = с. ?
6.2.2. Теорема. На множестве комплексных чисел можно определить отношение линейного порядка так, чтобы операция сложения была монотонной, но поле комплексных чисел нельзя превратить в упорядоченное поле.
Доказательство. На множестве комплексных чисел С определим отношение 2 = 1 — пришли к противоречию. Если /’ = 0, то — 1 = 1-0 — противоречие. Если же / 2 =-1, что снова ведет к противоречию. ?
