3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin х в виде бесконечного произведения
Ряды, члены которых являются простыми комбинациями целых чисел, особенно интересны. В качестве примера рассмотрим «гармонический ряд»
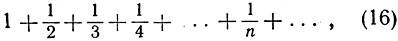
отличающийся от известного нам ряда, сумма которого равна ln 2, только знаками членов, стоящих на четных местах.
Поставить вопрос, сходится ли этот ряд, все равно, что спросить себя, стремится ли к конечному пределу последовательность чисел
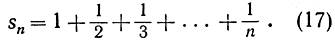
Несмотря на то что по мере продвижения по ряду (16) члены его приближаются к 0, легко увидеть, что ряд этот не сходится. Действительно, взяв достаточное количество членов, мы можем превысить любое положительное число; таким образом, sn возрастает беспредельно, и, значит, ряд (16) «расходится к бесконечности». Чтобы в этом убедиться,заметим, что
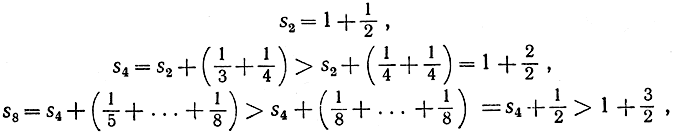
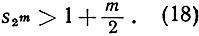
Таким образом, например, частные суммы s2 m превышают 100, если только m≥200.
Если гармонический ряд расходится, то, с другой стороны, можно доказать, что ряд
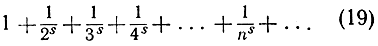
сходится при всяком значении s, большем, чем 1, и сумма его, рассматриваемая как функция переменного s, есть так называемая дзета-функция
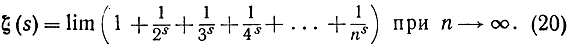
Эта функция, очевидно, определена только при s>1.
Существует важное соотношение между дзета-функцией и простыми числами, которое мы выведем, исходя из свойств геометрической прогрессии. Пусть р есть какое-нибудь простое число; тогда при s≥1
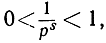
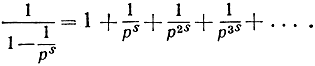
Перемножим такого рода равенства, написанные для всех простых чисел р = 2, 3, 5, 7, . (не задаваясь вопросом о законности такой операции). В левой части мы получим «бесконечное произведение»
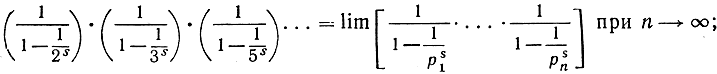
в то же время в правой части мы получаем ряд
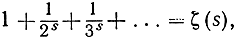
в силу того обстоятельства, что каждое целое число, большее, чем 1, может быть единственным образом представлено как произведение степеней различных простых чисел. Итак, нам удалось выразить дзета-функцию в виде произведения
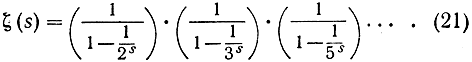
Если бы существовало только конечное число простых чисел, скажем, p1, p2, p3, . pr, то произведение в правой части формулы (21) было бы обыкновенным конечным произведением и имело бы поэтому конечное значение даже при s = 1. Однако мы видели, что дзета-ряд при s = 1
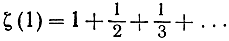
расходится, стремясь к бесконечности. Это рассуждение, которое легко превратить в строгое доказательство, показывает, что существует бесконечное множество простых чисел. Конечно, это доказательство гораздо запутаннее и искусственнее, чем данное Евклидом (см. стр. 46). Но оно столь же привлекательно, как трудный подъем на вершину горы, которая могла бы быть достигнута с другой стороны по комфортабельной дороге.
С помощью бесконечных произведений, подобных тому, которое дается формулой (21), функции иногда выражаются так же удобно, как и с помощью бесконечных рядов.
Другое бесконечное произведение, открытие которого представляет собой еще одно из достижений Эйлера, относится к тригонометрической функции sin х. Чтобы понять найденную Эйлером формулу, мы начнем со следующего замечания относительно многочленов. Если
есть многочлен степени n, имеющий n различных нулей х1, . хn, то, как известно из алгебры, функция f (x) может быть разложена на линейные множители
(см. стр. 129). Вынося за скобку произведение x1x2. xn, мы можем написать
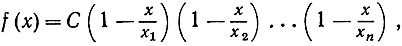
где С — постоянная, равная а, что легко установить, положив х = 0. Далее возникает вопрос: возможно ли аналогичное разложение уже не для полиномов, а для более сложных функций f(x)? (В общем случае ответ не может быть утвердительным, в чем легко убедиться на примере показательной функции, которая вовсе не имеет нулей, поскольку е x ≠0 при любых значениях х.) Эйлер открыл, что для функции синус такое разложение возможно. Чтобы написать формулу в ее простейшем виде, мы рассмотрим не sin x, a sin πx. Последняя функция имеет нулями точки π = 0, ±1, ±2, ±3, . так как sin πn = 0 при всех целых n; иных же нулей она не имеет никаких. Формула Эйлера устанавливает соотношение
Читайте также: Как поменять цвет батареи на айфоне
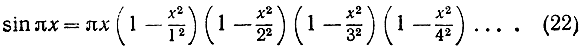
Стоящее справа бесконечное произведение сходится при всех значениях х и является одной из красивейших формул математики. При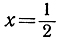 
формула дает
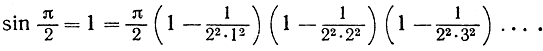
Если мы напишем
то после небольших преобразований получим произведение Уоллиса
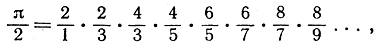
упомянутое на стр. 333.
За доказательствами всех этих соотношений мы вынуждены направить читателя к руководствам по анализу (см. также стр. 549-550).
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ — произведение бесконечного числа сомножителей , т. е. выражение вида … Большой Энциклопедический словарь
бесконечное произведение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN infinite product … Справочник технического переводчика
Бесконечное произведение — В математике для последовательности чисел бесконечное произведение определяется как предел частичных произведений при . Произведение называется сходящимся, когда предел существует и не равен нулю. Иначе произведение называется расходящимся.… … Википедия
бесконечное произведение — произведение бесконечного числа сомножителей u1, u2. un. то есть выражение вида: u1u2. un. = П∞k = 1 Uk * * * БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ, произведение бесконечного числа сомножителей , т. е. выражение вида … Энциклопедический словарь
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ — произведение бесконечного числа сомножителей и1 , и2, . иn, . т. е. выражение вида: u1u2. un. =Пk=1 uk … Естествознание. Энциклопедический словарь
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ — выражение содержащее бесконечное множество числовых или функциональных сомножителей, каждый из к рых отличен от нуля. Б. п. наз. сходящимся, если существует отличный от нуля предел последовательности частичных произведений при . 3начением Б. п.… … Математическая энциклопедия
ЭЙЛЕРА ПРОИЗВЕДЕНИЕ — бесконечное произведение вида где s действительное число и . пробегает все простые числа. Это произведение абсолютно сходится при всех s>1. Аналогичное произведение для комплексных чисел абсолютно сходится при и задает в этой области дзета… … Математическая энциклопедия
РИССА ПРОИЗВЕДЕНИЕ — бесконечное произведение вида для всех . С помощью таких произведений ( при всех ) Ф. Рисс (F. Riesz) указал первый пример непрерывной функции с ограниченным изменением, коэффициенты Фурье к рой не равны . Если q>3,то тождество определяет ряд… … Математическая энциклопедия
Прямое произведение — Прямое или декартово произведение множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих… … Википедия
Декартово произведение — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Эйлер последовательно рассмотрел два разложения функции синуса в ряд. Один из этих бесконечных рядов открыл сам Эйлер:
где знаменатели дробей — квадраты натуральных чисел, умноженные на квадрат числа 71. Второе разложение синуса в бесконечный ряд открыл Ньютон:
Читайте также: Как сбросить настройки андроид через компьютер
Здесь знаменатели представляют собой факториалы последовательных чисел. Напомним, что факториал произвольного числа n определяется как произведение всех чисел, меньших n: n·(n — 1)·(n — 2)· … ·3·2·1. Следовательно, знаменатели в представленной выше формуле равны факториалам показателя степени z плюс 1.
Иными словами, если показатель степени z равен 2, то знаменатель будет факториалом 3: 3·2·1 = 6; если показатель степени z равен 4, то знаменатель будет равен факториалу 5: 5·4·3·2·1 = 120, и так далее.
Так как оба этих ряда представляют собой разложение одной и той же функции синуса, они должны быть равны, в частности:
Согласно изложенному в предыдущем абзаце, получим:
или, что аналогично:
Таким образом, суммой чисел, обратных квадратам натуральных чисел, будет квадрат числа π, разделенный на 6.
Размышления Харди применительно к практике
Теперь вернемся к рассуждениям Харди о двух основных свойствах, которые наделяют математическую идею эстетической ценностью. Харди писал: «Два качества играют существенную роль: общность и глубина идеи, но ни одно из них не поддается определению легко и просто».
Говоря об общности математической идеи, Харди уточнял: «Значительная математическая идея, серьезная математическая теорема должна обладать «общностью» в каком-то следующем смысле. Идея должна быть составляющей частью многих математических конструкций, используемых в доказательствах многих теорем различного рода. Теорема должна быть такой, что даже если первоначально она сформулирована в весьма частном виде (как теорема Пифагора), она должна допускать существенное обобщение и быть типичной для целого класса теорем аналогичного рода. Отношения, выявляемые в ходе ее доказательства, должны связывать многие различные математические идеи». Чтобы у читателя не осталось никаких сомнений относительно того, насколько сложно точно определить «общность», Харди писал: «Всё это очень смутно и требует многочисленных уточнений».
Рассмотрим пример, приведенный Эйлером: обладает ли ряд Эйлера общностью в том смысле, в каком трактовал это свойство Харди? Да, этот ряд действительно обладает общностью, причем в нескольких значениях.
Основная идея Эйлера заключалась в том, чтобы использовать для вычисления некоторых бесконечных сумм два представления одной и той же функции: одно в виде произведения, другое — в форме ряда. В представленном выше случае Эйлер с помощью функции синуса нашел сумму чисел, обратных квадратам натуральных чисел. Применив другие функции, Эйлер во «Введении в анализ бесконечно малых» с помощью аналогичного метода вычислил множество сумм бесконечных рядов, в частности:
В этой сумме с противоположными знаками записаны числа, обратные кубам нечетных чисел, за исключением кратных 3.
Однако общность идеи Эйлера не ограничивается одной лишь заменой функции синуса на другие. В его методе рассматривается выражение
Число, на которое последовательно умножается z 2 , связывается с суммой чисел, на которые умножается z 2 в левой части равенства. В слегка видоизмененном виде идея Эйлера становится еще более плодотворной. Достаточно обратить внимание на числа, которые умножаются на остальные степени переменной в правой части равенства и выразить их через коэффициенты при z 2 в левой части равенства (см. врезку на следующей странице). Применив эту идею, Эйлер вычислил не только сумму чисел, обратных квадратам натуральных чисел, но и чисел, обратных четвертым, шестым и восьмым степеням:
Ему удалось дойти до 26-й степени:
Читайте также: Динамическая контрастность mega что это
Надеемся, что читатель смог оценить всю общность рассуждений Эйлера и, как следствие, лучше понять, что хотел сказать Харди, когда писал об общности математической идеи: именно общностью, помимо гениальности, отличается рассмотренная идея Эйлера.
Согласно Харди, другое неотъемлемое свойство, наделяющее математическую идею эстетической ценностью, — это глубина. «Второе свойство, которое я потребовал от значительной идеи, — ее глубина. Определить его еще труднее. Оно каким-то образом связано с трудностью; «более глубокие» идеи обычно труднее постичь, но вместе с тем это не одно и то же. Создается впечатление, что математические идеи «стратифицированы», то есть расположены как бы слоями, идеи в каждом слое связаны целым комплексом отношений между собой и с идеями, лежащими в верхних и нижних слоях. Чем ниже слой, тем глубже (и, как правило, труднее) идея».
ЭЙЛЕР И БЕСКОНЕЧНЫЕ РЯДЫ
Эйлер уточнил свою исходную идею следующим образом. Вернемся к произведению
(1 — az 2 )·(1 — bz 2 )·(1 — cz 2 )·… = 1 — Az 2 + Bz 4 — Cz 6 +…
Теперь рассмотрим число 8, на которое умножается z 4 . Нетрудно видеть, что это число В образуется попарным умножением с последующим сложением чисел а, Ь, с которые умножаются на z 2 в левой части равенства: B = ab + ac + bc + …
Таким образом, если мы запишем Р = а + Ь + с +… и Q = а 2 + Ь 2 + с 2 + …. путем простых подсчетов имеем: Р = A и Q = A·P — 2·B.
Если мы вновь рассмотрим два разложения для функции синуса:
и примем во внимание, что в этом случае А = 1/6, B = 1/120 и, как мы уже вычислили, Р = π 2 /6, получим значение суммы чисел, обратных четвертым степеням натуральных чисел: 1 + 1/24 + 1/34 + 1/44 + … = π4 /90.
Нечто подобное можно выполнить для z 6 и последующих степеней. Благодаря этому Эйлер вычислил суммы чисел, обратных четным степеням натуральных чисел, начиная от второй и заканчивая двадцать шестой. Несколько лет спустя Эйлер обнаружил общую формулу суммы чисел, обратных произвольной четной степени натуральных чисел. О сумме чисел, обратных нечетным степеням натуральных чисел, ничего не известно и поныне. Мы знаем лишь, что первые несколько подобных сумм являются иррациональными числами.
И вновь суммы Эйлера помогут нам понять, что Харди имел в виду, когда говорил о «глубине» математических идей. Эйлер связал математические понятия из разных областей. В методе Эйлера скрывается понятие бесконечности, принадлежащее, можно сказать, к метафизике. Этот метод относится и к арифметике, так как в его задаче рассматриваются натуральные числа — требуется сложить квадраты чисел, обратных им. При вычислении суммы на сцену выходит геометрия, так как значение суммы выражается с помощью квадрата числа π, описывающего геометрию окружности. Наконец, весь метод Эйлера вращается вокруг представления функции в виде бесконечной суммы и бесконечного произведения — эти методы относятся к математическому анализу. И все это богатство взаимосвязей между столь разными «стратами» проявилось в одной идее Эйлера, которая на первый взгляд кажется простой. Именно это имел в виду Харди, когда говорил о глубине идеи: он рассуждал о ее способности неизбежно и плодотворно самым блестящим образом связывать между собой разные математические «страты».
