
Одной из самых распространённых задач является выявление в спектре сигнала составляющих. Делается это для того чтобы отфильтровать сигнал. Ведь иногда по одной линии передаётся далеко не один сигнал, в то время как обрабатывать каждый из них нужно по разному.
Рассмотрим простейший случай такого анализа в Matlab.
Сформируем временную сетку:
Теперь зададим сигнал для тренировок:

Как видите это всего навсего 2 синусоиды. одна на частоте 50Гц, другая на 120Гц. В жизни такого конечно же нет. Это всего навсего математическая абстракция, которая поможет понять как всё происходит.
Выведем сигнал для наглядности:
Теперь делаем преобразование Фурье для нашего сигнала.
Имеем 512 отсчётов. Примем это во внимание для нахождения цифрового преобразования:
Домножим на комплексно сопряженное и нормализуем:
Теперь задаём сетку частот и выводим спектр:

Как видно на рисунке, в спектре имеется 2 выброса на частотах 50 и 120Гц. Что подтверждается частотами, которые мы задали.
Отмечу ещё раз, что это идеальная ситуация, которой в жизни никогда не бывает. В настоящем сигнале постоянно присутствуют помехи с самыми разными частотами, что существенно зашумляет спектр и делает его менее наглядным.
В программе Simulink можно производить анализ спектра методом ДПФ (дискретного преобразования Фурье). При этом возможно анализировать спектры только непериодических сигналов по конечным наборам отсчетов.
Для анализа спектра периодических сигналов более целесообразно использовать функции классического языка MATLAB. Однако в этом случае моделирование спектра напоминает работу в программе Mathcad.
Работа в программе MATLAB осуществляется с помощью симулятора работы виртуального прибора Simulink. Запуск пакета Simulink можно произвести из командного окна MATLAB, нажав пиктограмму  в панели инструментов и открыв новую модель (пиктограмма
в панели инструментов и открыв новую модель (пиктограмма ).
).
При запуске Simulink открываются два окна: пустое окно untitled (окно для создания блок–диаграммы модели) и окно Library Simulink (библиотека) с перечнем основных разделов библиотеки.
В открывшееся окно untitled необходимо добавить блоки, моделирующие работу источников сигналов, измерительных приборов и аналоговых систем.
Для изменения параметров блоков необходимо выполнить двойной щелчок на пиктограмму блока. При этом должно открыться окно настройки параметров Block Parameters.
Создание модели фильтра
Для проведения спектрального анализа аналогового фильтра требуется составить следующую структурную схему (модель), рис. 5.
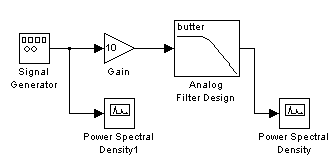
Рис. 5. Структурная схема для проведения спектрального анализа фильтра
Модель аналогового фильтра (в данной работе исследуется фильтр Баттерворта) выглядит так, как показано на рис. 6, и создается с помощью следующих блоков:
аналоговый фильтр с единичным усилением Analog Filter Design
(DSP blockset/Filtering/Filter Design/Analog Filter Design), рис. 7;
усилитель Gain (Simulink/Math/Gain), рис. 8.

Рис. 6. Модель фильтра Баттерворта в программе MATLAB
Рис. 7. Расположение блока Analog Filter Design

Рис. 8. Расположение блока усилителя Gain
Исходные данные необходимые для синтеза аналогового фильтра:
порядок фильтра N;
пульсации в полосе пропускания / заграждения (не требуется для фильтров Баттерворта);
коэффициент усиления K.
Исходные данные задаются в блоке параметров фильтра Block Parameters: Analog Filter Design (рис. 9), где:
Читайте также: Windows 10 не открывается календарь
Design method – вид аппроксимации;
Filter order – порядок фильтра.
Коэффициент усиления задается отдельно в блоке параметров усилителя Block Parameters: Gain (рис. 10).
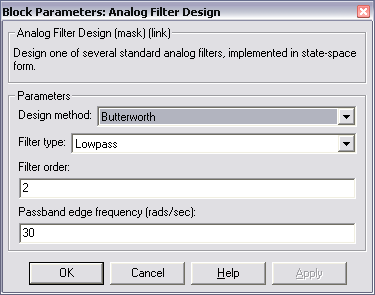
Рис. 9. Блок параметров Analog Filter Design
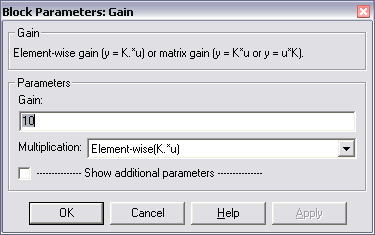
Рис. 10. Окно настройки параметров блока Gain
Блок Power Spectral Density (анализатор спектра)
Для просмотра спектральной плотности сигнала используют анализаторы спектра Power Spectral Density (Simulink Extras/Additional Sinks/Power Spectral Density), рис.11.
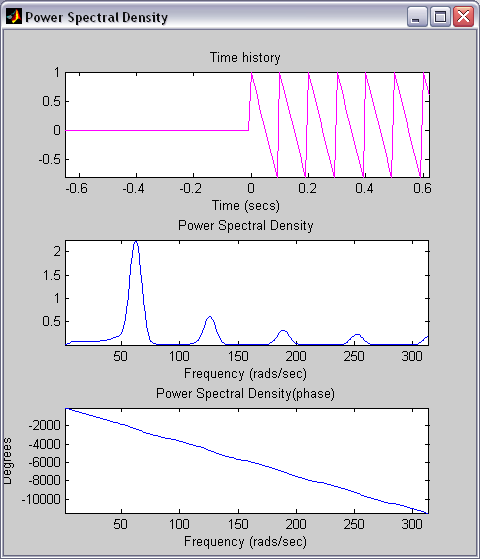
Рис. 11. Расположение блока Power Spectral Density (а) и результаты анализа спектра (б)
В окне настройки Block Parameters: Power Spectral Density, рис. 12, задаются следующие параметры анализатора спектра:
Length of buffer – длина буфера (по умолчанию 128);
Number of points for fft – число анализируемых точек (по умолчанию 512);
Plot after how many points– количество точек, после которого производится построение графика (по умолчанию 64);
Sample time – период дискретизации.
Все параметры, кроме периода дискретизации, должны быть кратны 2 N , где N – целое число.

Рис. 12. Окно настройки параметров блока Power Spectral Density
Результаты анализа спектра, выполняемого блоком Power Spectral Density, представляются в трех окнах (рис. 11.б):
исследуемый сигнал (Time history);
амплитудный спектр (Power Spectral Density);
фазовый спектр (Power Spectral Density (phase)).
Чтобы просмотреть спектр сигнала нужно запустить работу модели. Это можно сделать, вызвав меню Simulation и нажав команду Start, либо нажав сочетание клавиш Ctrl + T или же щелкнув пиктограмму  –Start simulation.
–Start simulation.
Блок Signal Generator (генератор сигналов)
Для задания гармонического сигнала, используется блок Signal Generator
(Simulink/ Sources/Signal Generator), рис. 13.
Рис. 13. Расположение блока Signal Generator
В окне настройки блока Signal Generator задаются следующие параметры:
Wave form – форма сигнала:
sine– синусоидальный сигнал;
square – прямоугольный сигнал;
saw tooth – пилообразный сигнал;
random – случайный сигнал (шум);
Amplitude и Frequency – амплитуда и частота сигнала;
Units – единица измерения частоты (Hertz – Герцы или rad/sec – рад/сек).

Рис. 14. Окно настройки параметров блока Signal Generator
Для создания более сложных сигналов используется сумматор (Simulink/ Math Operations/Sum), рис. 15. Блок Sum выполняет суммирование входных сигналов. Пример использования сумматора для сложения двух входных сигналов показан на рис. 16.
Рис. 15. Расположение блока Sum

Рис. 16. Пример использования сумматора для сложения двух сигналов
Сумматор может использоваться в двух режимах:
Сложение входных сигналов (в том числе с разными знаками);
Суммирование элементов вектора, поступающих на вход блока.
Окно настройки параметров блока Sum изображено на рис. 18. Вводя значения в поле List of sings (список знаков), можно управлять режимами работы блока Sum.
Значения могут задаваться одним из трех способов:
в виде последовательности знаков «+» и «–», причем число знаков определяет число входов блока, а сами знаки – полярности соответствующих входных сигналов. При большом количестве слагаемых их целесообразно разбить на несколько групп, отделяя одну группу от другой символом │ (например: + +│– +);
Читайте также: Правила переноса слов через дефис
в виде целой положительной константы (больше 1), значение которой равно числу входов блока, а все входы считаются положительными (например, ввод константы 4 аналогичен вводу «списка знаков» в форме + + + +).
ввод значении 1 означает вычисление суммы элементов входного вектора (в этом случае внутри блока выводится символ ?).
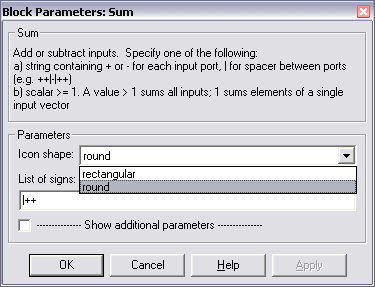
Рис. 17. Окно настройки параметров блока Sum
Два других параметра настройки блока имеют следующий смысл:
раскрывающийся список Icon shape (форма значка) позволяет выбрать форму блока: round (окружность) или rectangular (прямоугольник);
флажок Show additional parameters (показать дополнительные параметры) дает возможность задать необходимость «усечения» результата сложения, если он превышает диапазон, установленный для целочисленных значений.
Режимы моделирования систем в программе Simulink (меню Simulation)
Посредством этих команд входящих в меню Simulation (моделирование), рис. 18, разработчик получает возможность не только динамически управлять сеансом моделирования, но и изменять многие важнейшие параметры модели, такие, например, как способ изменения модельного времени, алгоритм расчета и формат представления результатов моделирования.
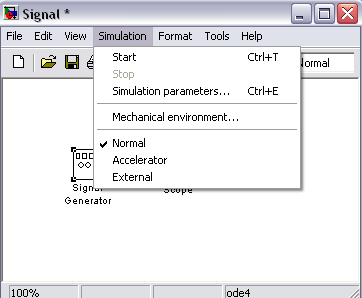
Рис. 18. Меню Simulation
Элементы управления на вкладке Solver окна Simulation Parameters (параметры моделирования), рис. 19, собраны в три группы.
Simulation time (интервал моделирования) – выбор интервала моделирования посредством указания начального (Start time) и конечного (Stop time) значений модельного времени.
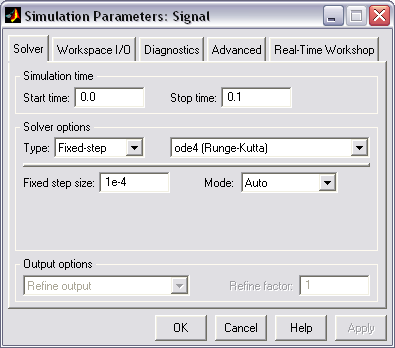
Рис. 19. Окно установки параметров моделирования
Solver options (параметры расчета) – выбор метода реализации (расчета) модели.
Output options (параметры вывода) – параметры вывода выходных параметров моделируемой системы (при моделировании с переменным шагом).
Под выбором метода реализации модели имеется в виду следующее. Имея структуру исследуемой системы в виде блок–диаграммы, разработчик может выбрать метод отображения хода моделирования. С помощью двух раскладывающихся списков Type (тип) система может быть реализована в следующих формах:
с дискретными состояниями и дискретным временем перехода из одного состояния в другое;
с дискретными состояниями и непрерывным временем перехода;
с непрерывными состояниями и дискретным временем переходов;
с непрерывными состояниями и непрерывным временем переходов.
Первый список (слева) позволяет выбрать способ изменения модельного времени:
Variable – step (переменный шаг) – моделирование с переменным шагом;
Fixed – step (фиксированный шаг) – моделирование с фиксированным шагом.
Второй список (справа) позволяет выбрать метод расчета нового состояния системы. Первый вариант (discrete) обеспечивает расчет дискретных состояний системы. Остальные пункты списка обеспечивают выбор метода расчета нового состояния для непрерывных систем. Эти методы различаются для переменного (Variable – step) и для фиксированного (Fixed – step) шага времени, но основаны на единой методике – решение обыкновенных дифференциальных уравнений(ode).
Ниже двух раскрывающихся списков Type находится поле, название которого изменяется в зависимости от выбранного способа изменения модельного времени.
Параметры других вкладок используется по умолчанию.
Читайте также: Бренди ла форет хо
Страницы работы




Содержание работы
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 2
Студент: Першина Ж. С.
Преподаватель: доц. Щетинин Ю. И.
Изучение понятия спектра периодического сигнала, приобретение практических навыков вычисления и построения графиков спектров сигналов в среде MATLAB.
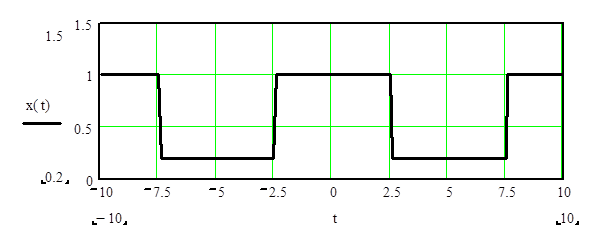
Рис. 1. Спектр периодической последовательности прямоугольных импульсов.
Ряд Фурье 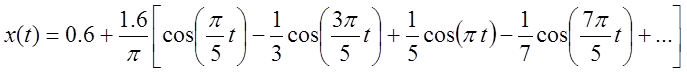
· Функция: 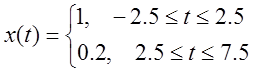 ;
;
· Частота основной гармоники: ω0=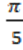 .
.
1. Коэффициенты комплексного ряда Фурье (аналитический метод).
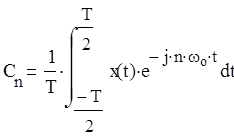
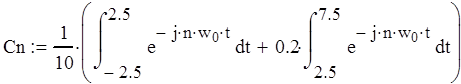
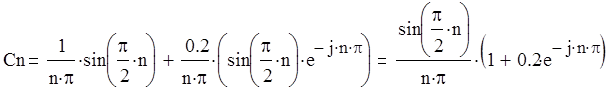
|C1|=0.255, |C2|=0, |C3|=0.085, |C4 |=0, |C5 |=0.051
Так как данная функция является четной, все коэффициенты bn=0.
2. Файл-сценарий для построения графиков амплитудного и фазового спектров сигнала в Matlab.
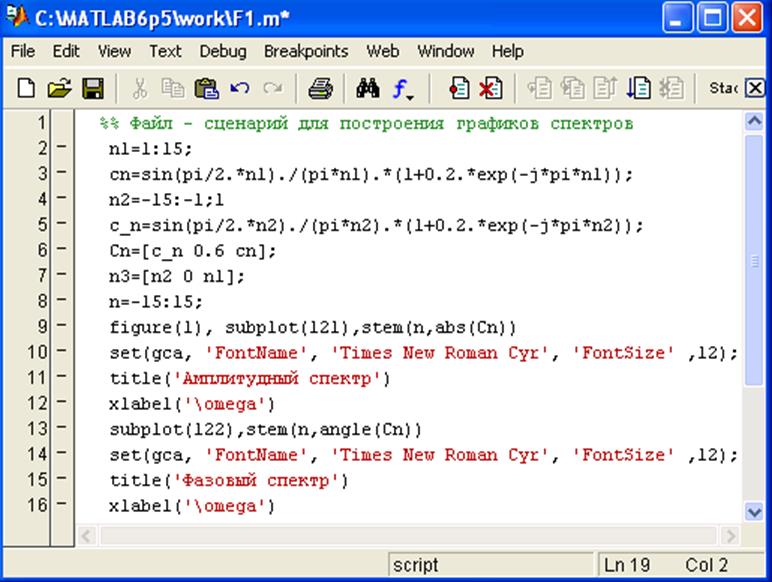
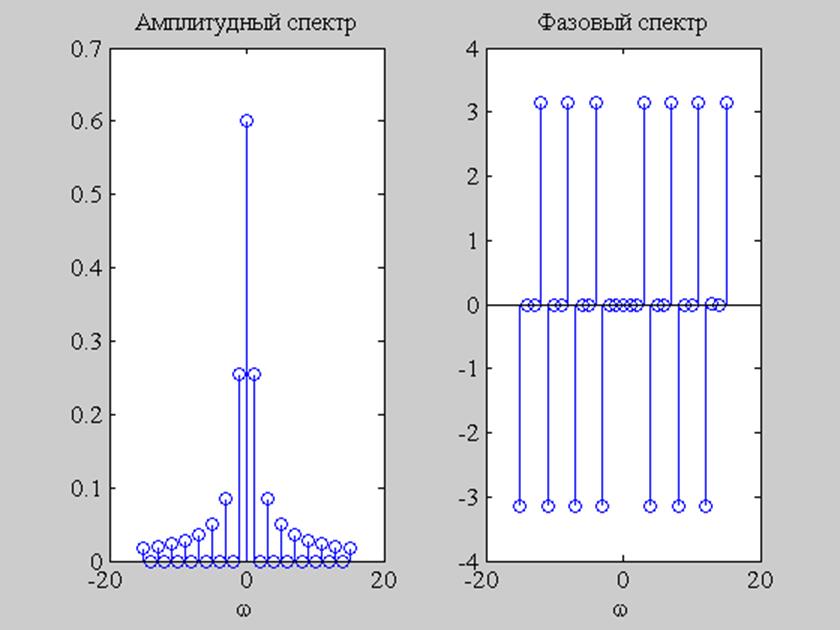
Рис.2. Графики амплитудного и фазового спектров сигнала.
3. Определение спектра Фурье сигнала с помощью функции fft() Matlab.
%файл-сценарий для вычисления коэффициентов ряда Фурье сигнала с помощью процедуры fft()
T=10; % период сигнала
t=-T:T/63:T; % временной интервал
x=0.4*square(2*pi*(t+2.5)./N,50)+0.6; % генерирование сигнала
subplot(311), plot(t,x) % график сигнала
set(gca, ‘FontName’, ‘Times New Roman Cyr’, ‘FontSize’ ,12);
% коэффициенты ряда Фурье
% график амплитудного спектра
set(gca, ‘FontName’, ‘Times New Roman Cyr’, ‘FontSize’ ,12);
y=fft(x,64);% Дискретное преобразование Фурье сигнала
subplot(313), stem(2*pi*k/T, abs(y)/64)
set(gca, ‘FontName’, ‘Times New Roman Cyr’, ‘FontSize’ ,12);
title(‘Амплитудный спектр по команде fft()’)
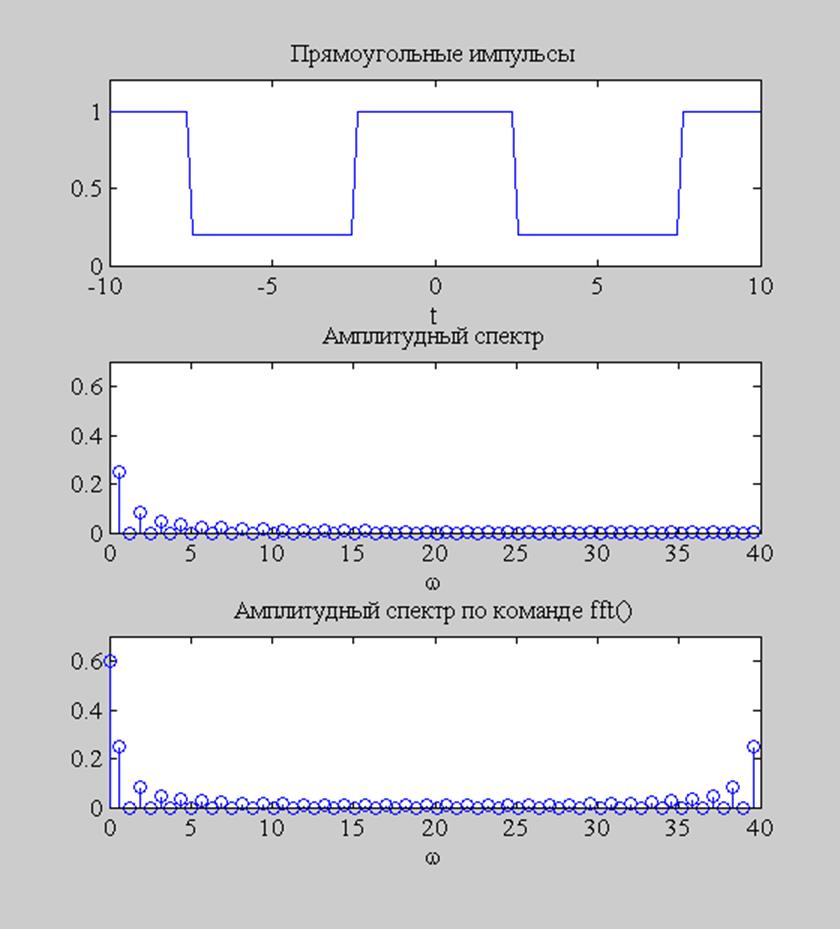
Рис. 3. График сигнала и графики его амплитудных спектров.
Переделать второй график: не хватает постоянной составляющей сигнала.
5.Составление и выполнение файл-сценария для исследования сходимости ряда Фурье.
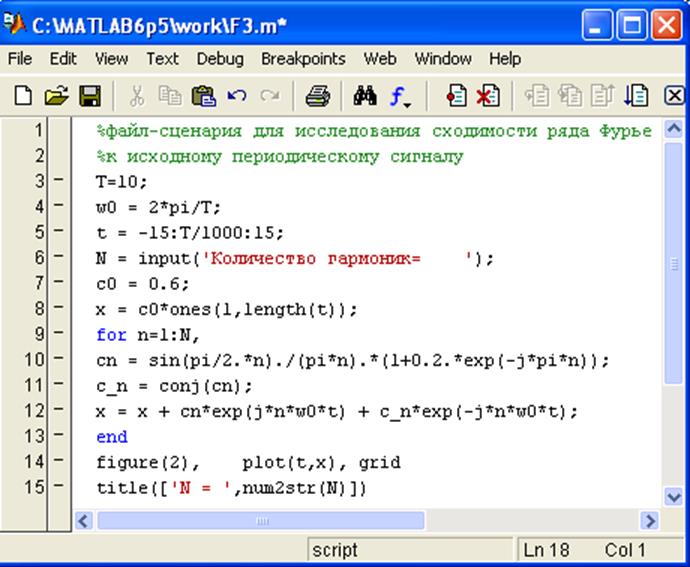
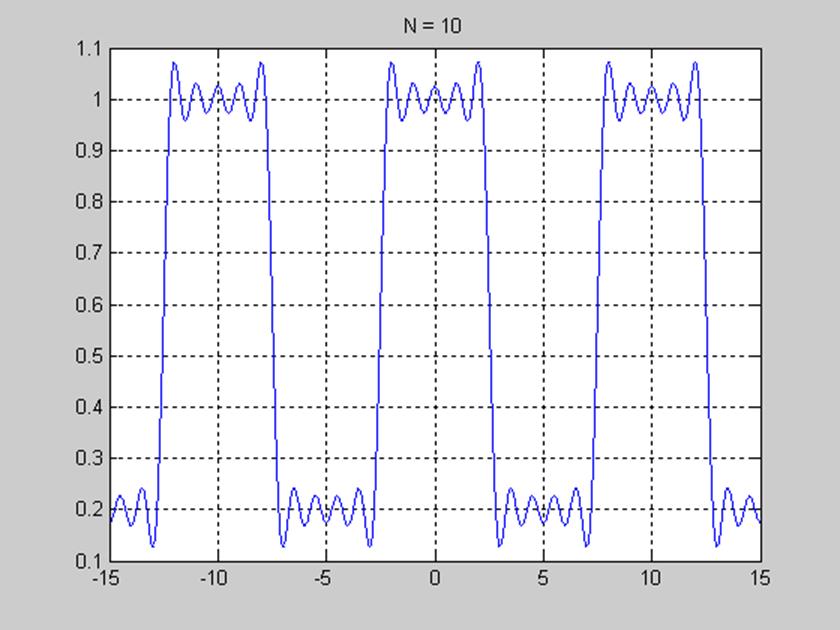
Рис. 4. График, отображающий явление Гиббса десятью гармониками.
Не помешало бы для наглядности сходимости на рис.4 отобразить исходный сигнал.
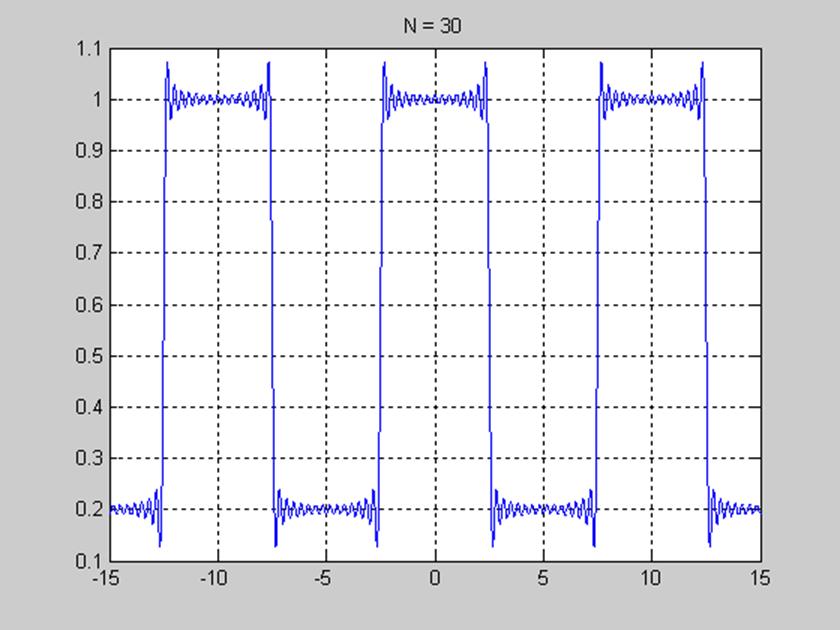
Рис. 5. График, отображающий явление Гиббса тридцатью гармониками.
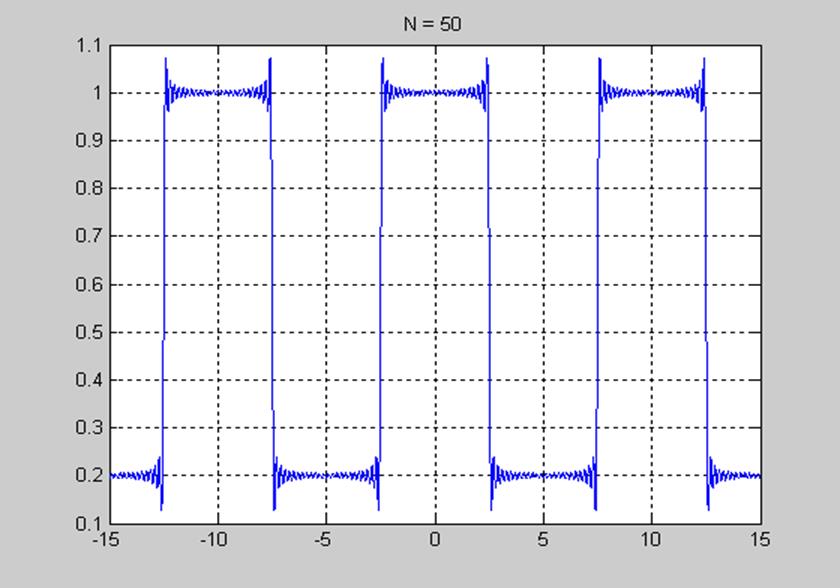
Рис. 6. График, отображающий явление Гиббса пятидесятью гармониками.
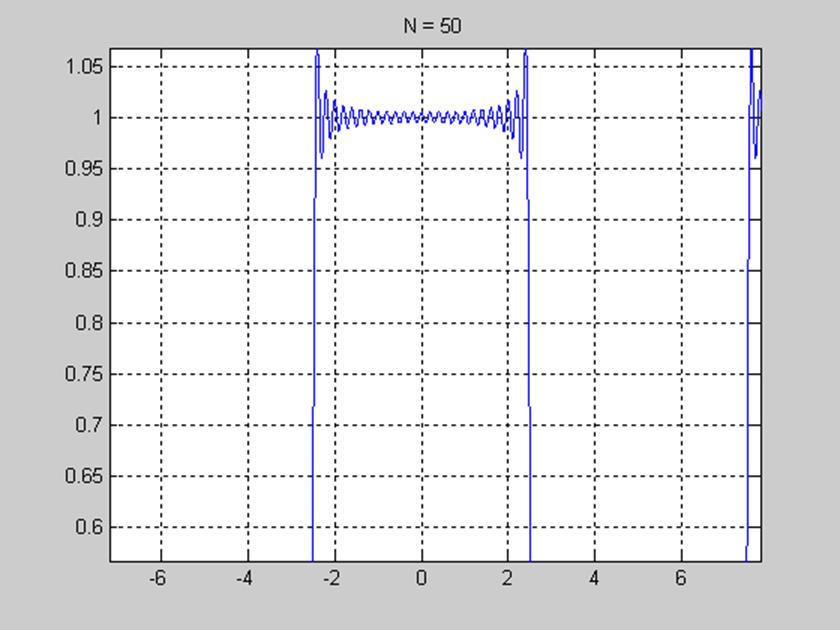
Рис. 7. График, отображающий явление Гиббса пятидесятью гармониками (увелич. Масштаб).
Явление Гиббса – это явление связанное с появлением пульсации или выбросов при суммировании рядов Фурье. От числа гармоник N зависит число выбросов, амплитуда выбросов не зависит от числа гармоник.
Отобразить свойства сходимости, рассмотрев среднеквадратичную сходимость и …
6. Аппроксимации сигналов: квадратной волны, ноты Ре, ноты До.
x = x + 4*sin(w0*n*t)/(pi*n);
>> y=harmonic(w0, 2*pi*8192, 2);
>> axis([0 0.012 -1.5 1.5]);
>> p = zeros(1,length(t)); p=[x p y];

Рис. 8. График аппроксимации ноты Ре.
do = do + k(n)*sin(n*w0*t);
>> subplot(211), plot(t(1:100),do(1:100)) , grid
>> axis([0 0.012 -1.5 1.5]);
>> set(gca, ‘FontName’, ‘Times New Roman Cyr’, ‘FontSize’ ,12);
>> title(‘График ноты До’);
>> subplot(212), stem(2*pi*s/T, abs(y)/(N+1)), grid
>> axis([0 max(2*pi*s/T)/2 0 max(abs(y)/(N+1))]);
>> set(gca, ‘FontName’, ‘Times New Roman Cyr’, ‘FontSize’ ,12);
>> xlabel(‘ Угловая частота, рад/сек’)
>> title(‘ Амплитудный спектр ноты До по процедуре fft’)
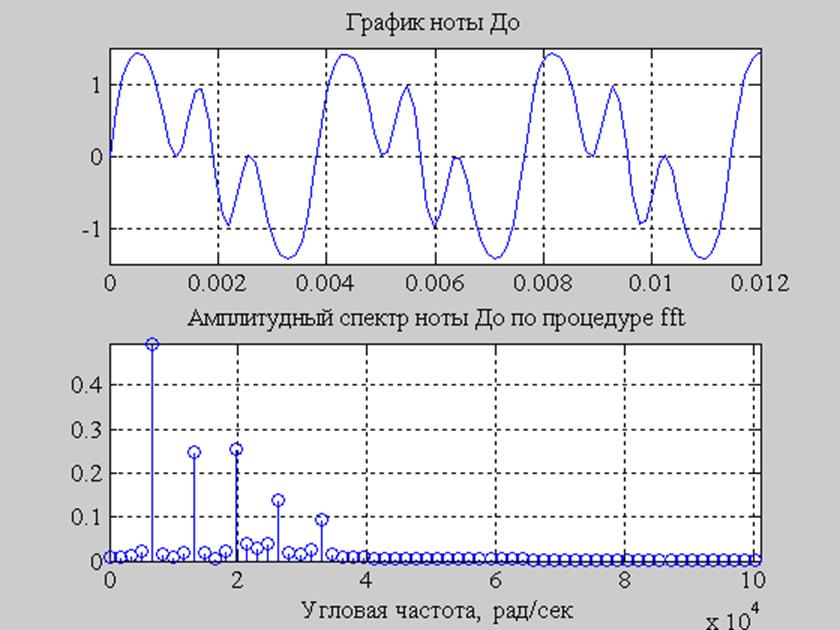
Рис.9. График ноты До и его амплитудный спектр.
Вывод: в данной работе было изучено спектральное представление периодических сигналов на примере периодической последовательности прямоугольных импульсов, при исследования сходимости ряда Фурье к исходному периодическому сигналу было рассмотрено явление Гиббса.
. Подробное описание основных моментов работы.








